Effects of terrain features on wave propagation: high-frequency techniques

(1)

Effects of terrain features on wave propagation:

high-frequency techniques

M. Sarwar

Submitted for the Degree of

Master of Science in Electrical Engineering

Department of Technology

University of Kalmar

S-391 82 Kalmar SWEDEN

(2)

Abstract

This Master thesis deals with wave propagation and starts with wave propagation basics. It briefly presents the theory for the diffraction over terrain obstacles and describes two different path loss models, the Hata model and a FFT-based model. The significance of this paper is that it gives the simulation results for the models mentioned above and presents a comparison between the results obtained from an empirical formula and the FFT-model. The comparison shows that the approach based on Fast Fourier Transform is good enough for prediction of the path loss and that it is a time efficient method.

Keywords: wave propagation, path loss, Hata model, half-screen, FFT-model.

Email: ms22jy@student.hik.se

(3)

Acknowledgments

I would like to thank my supervisor Sven-Erik Sandström, Lecturer in School of Mathematics and Systems Engineering, Växjö University for his support throughout the Master thesis work. I also appreciate to Magnus Nilsson and other lecturers in the Department of Technology, University of Kalmar, where this thesis work was performed. And finally, I am very grateful to my family and friends, who always help me whenever I need.

(4)

TABLE OF CONTENTS

1. INTRODUCTION ... 1

2. THEORETICAL BACKGROUND... 3

2.1 BASIC PROPAGATION THEORY ... 3

2.1.1 Specular Reflection ... 4

2.1.2 Scattering ... 4

2.1.3 Diffraction... 4

2.1.4 Multiple Diffraction ... 7

2.2 PATH LOSS MODELS ... 8

2.2.1 The Hata Model ... 8

2.2.2 The FFT based Model ... 9

3. SIMULATION... 12

3.1 THE HATA MODEL ... 12

3.2 AN FFT BASED MODEL... 15

3.3 COMPARISON OF THE SIMULATION RESULTS FOR THE HATA MODEL AND THE FFT BASED MODEL... 17

4. CONCLUSION... 20

REFERENCES ... 21

APPENDIX A... 22

APPENDIX B ... 25

(5)

1. INTRODUCTION

The aim of this thesis work is to present the theory as well as the implementation of different models for predicting the path loss between a base station antenna and mobile station antennas. The prediction of path loss is a very important step in planning a mobile radio system and accurate prediction methods are needed to determine the parameters of a radio system which will provide efficient and reliable coverage of a specified service area [1]. In order to make these predictions one should understand the factors that influence the signal strength. For instance, the effects of buildings and other obstacles should be considered in an urban area. In rural places, shadowing, scattering and absorption by trees and other vegetation can cause great path losses, especially at higher frequencies.

One of the most common models for path loss prediction is the empirical model derived by Hata [2]. Due to its reliability the Hata model serves as a check for the FFT-model discussed in this work. The latter is based on a theoretical model called the half-screen model [3]. This means that buildings are replaced by absorbing screens of vanishing thickness. The propagating electric field is then treated by means of multiple diffraction, where reflections are not considered.

Due to the complexity of exact prediction of the propagation of the electric field there are some simplifications introduced in the current paper. The main limitation is that this thesis work treats the scalar electric field and not the vector electric field.

The current thesis work is similar to [3] and [6]. The difference with [3] is that it presents the affect of the various screen separation distances on the absolute path loss level. The difference with [6] is that it treats the case when the base station antenna height is equal 50 m, the screen separation distance is increased to 150 m and the simulation results are verified using MATLAB.

The thesis first presents a brief discussion of the wave propagation and diffraction theory in Chapter 2. It also contains two models for the propagation loss. In Chapter 3, these models are

(6)

Chapter 4 presents some concluding remarks. The codes and scripts for simulating the models are enclosed in appendices.

(7)

2. THEORETICAL BACKGROUND

2.1 BASIC PROPAGATION THEORY

The phenomena that influence radio wave propagation can generally be described by three basic mechanisms: reflection, diffraction, and scattering. The propagation mechanisms need to be studied for the development of propagation prediction models. The wave propagation phenomena depend on the environment and differ whether one considers flat terrain covered with grass, brick houses in a suburban area, or buildings in a modern city. Propagation models are more efficient when only the most dominant phenomena are taken into account. Which radio propagation phenomena to consider, and to what extent, depends on whether one is interested in modelling the average signal strength, fading statistics, the delay spread or some other entity.

A number of factors complicate the investigation of propagation phenomena:

1. The distance between a base station and a mobile could range from some meters to several kilometers.

2. Man-made objects and natural features have sizes ranging from much smaller than a wavelength to much larger than a wavelength and this affects the propagation of radio waves.

There are two approaches which can deal with these difficulties:

• Experimental investigations which are closer to reality but at the expense of weaker control on the environment.

• Theoretical investigations which consider only simplified model of the reality but give an excellent control of the environment.

The problem of designing the experiments, and the interpretation of the results, are the major disadvantages of experimental investigations. Software simulation has one main advantage over experimental investigations: the environment and the geometry are more easily described and

(8)

2.1.1 Specular Reflection

The specular reflection phenomenon is the mechanism by which a ray is reflected at an angle equal to the incidence angle. The reflected wave fields are related to the incident wave fields through a reflection coefficient. The most common expression for the reflection is the Fresnel reflection coefficient which is valid for an infinite boundary between two media, for example air and concrete. The Fresnel reflection coefficient depends on the polarization and the wavelength of the incident wave field and on the permittivity and conductivity of each medium. The use of the Fresnel reflection coefficient formulas is very popular in ray tracing software tools.

In some books the reflection coefficients are considered to be constant to simplify the computations. However the validity of a constant reflection coefficient is usually not investigated.

Specular reflections are mainly used to model reflection from the ground surface and from building walls.

2.1.2 Scattering

Rough surfaces and finite surfaces scatter the incident energy in all directions with a radiation diagram that depends on the roughness and the size of the surface or volume. The dispersion of energy through scattering entails a reduction of the energy reflected in the specular direction. A simple method to account for the diffuse scattering is to reduce the coefficient by multiplying with a factor smaller than one which depends exponentially on the standard deviation of the surface roughness according to the Raleigh theory. This description does not take into account the true dispersion of radio energy in various directions, but accounts for the reduction of energy in the specular direction due to the diffuse components scattered in all other directions.

2.1.3 Diffraction

Diffraction allows radio signals to propagate around the curved surface of the earth, beyond the horizon, and to propagate behind obstructions. Although the received field strength

(9)

decreases rapidly as a receiver moves deeper into the obstructed (shadowed) region, the diffraction field still exists and often has sufficient strength to produce a useful signal [4].

The phenomenon of diffraction is explained by Huygen’s principle, which states that all points on a wavefront can be considered as point sources for the production of secondary wavelets, and that these wavelets combine to produce a new wavefront in the direction of propagation. Diffraction is caused by the propagation of secondary wavelets into a shadowed region.

Consider a transmitter T and a receiver R separated by a distance d +₁ d₂ as shown in Figure 2.1.1 found in [1], page 35. The plane is normal to the line-of-sight path at a point between T and R. On this plane we construct concentric circles of arbitrary radius and it is apparent that any wave which has propagated from T to R via a point on any of these circles has traversed a longer path TOR.

Figure 2.1.1 − Concentric circles defining the limits of the Fresnel zones at a given point on the propagation path.

The difference between the direct path and the diffracted path, called the excess path length (∆), can be determined from the geometry of Figure 2.1.2 assuming that h <<d₁, d₂ and h>>λ (where h is the height of the obstructing screen). Thus, the excess path length is,

(

)

2 1 2 1 2 2 d d d d h + ⋅ ≈ ∆ . (2.1.1)

(10)

Figure 2.1.2 − The geometry of knife-edge diffraction. The corresponding phase difference,

(

)

2 1 2 1 2 2 2 2 d d d d h + ≈ ∆ =

λ

π

λ

π

φ

. (2.1.2)

Equation (2.1.2) is often normalized using the dimensionless Fresnel-Kirchoff diffraction parameter v which is given by,

(

)

2 1 2 1 2 d d d d h

λ

ν

= + . (2.1.3)

Hence, the phase difference can be expressed as,

2

2v π

φ = . (2.1.4)

The total path loss from T to R can be computed as

(Ltot)dB = (Lfs)dB + (Lke)dB, (2.1.5)

where Lfs is the free space loss between T and R (if no obstacle had been present) and Lke is the

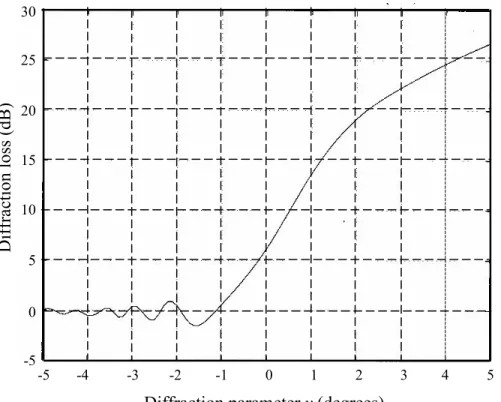
knife-edge diffraction loss. This loss can be obtained as a function of the diffraction parameter v, as shown in Figure 2.1.3 found in [5], page 55.

(11)

Figure 2.1.3 − Diffraction loss as a function of the diffraction parameter v.

2.1.4 Multiple Diffraction

In reality, the propagation path may consist of more than one obstruction. In such cases the total diffraction loss due to all obstacles must be computed. There are several approximate methods available in literature [1]. Bullington suggested to replace the series of obstacles with a single equivalent obstacle so that the path loss can be obtained using single knife-edge diffraction model. Bullington’s method has the advantage of simplicity but important obstacles below the paths of the horizon rays are sometimes ignored and this can cause large errors to occur. The limitation of the Bullington method is overcome by the Epstein-Peterson method; this method computes the attenuation due to each obstacle in turn and sums them to obtain the overall loss. Another method is the Deygout method, in which the path loss is estimated by considering the dominant knife-edge. The other losses, due to remaining knife-edges, are determined with respect to the dominant edge.

D if fr ac ti o n l o ss ( d B ) 30 25 15 20 10 5 0 -5

Diffraction parameter v (degrees)

(12)

2.2 PATH LOSS MODELS

The proposed path loss prediction models are the Hata model and the FFT based model, for which a brief theoretical description is given below.

2.2.1 The Hata Model

Path loss estimation is performed by using empirical models, if land cover is known only roughly, so that the parameters required for semi-deterministic models cannot be determined. Four parameters are used when estimating propagation loss with the Hata model [2]: frequency f , distance d, base station antenna height _c h and the height of the mobile antenna _b h . _m In the Hata model, which is based on Okumura’s various correction functions, the basic transmission loss in urban areas is given by,

( )

dB f h a

( ) (

h h

)

d

L_p =69.55+26.16log _c −13.82log _b − _m + 44.9−6.55log _b log . (2.3.1) For a large sized city, the mobile antenna correction factor is given by,

( )

h_m =3.2

(

log11.75h_m

)

2 −4.97

a . (2.3.2)

The practical range for the parameters is,

c f : 150 MHz to 1500 MHz b h : 30 m to 200 m m h : 1 m to 10 m d : 1 km to 20 km

To obtain the path loss in suburban area, the standard Hata formula is modified as,

( )

=

_p

( )

−

2 [

log

(

_c

/

28 )

]

2

−

5 .

4

ps

dB

L

dB

f

L

. (2.3.3)

And for the path loss in open rural areas, the formula is modified as,

( )

= _p

( )

−4.78

(

log _c

)

2 +18.33log _c−40.94

po dB L dB f f

(13)

2.2.2 The FFT based Model

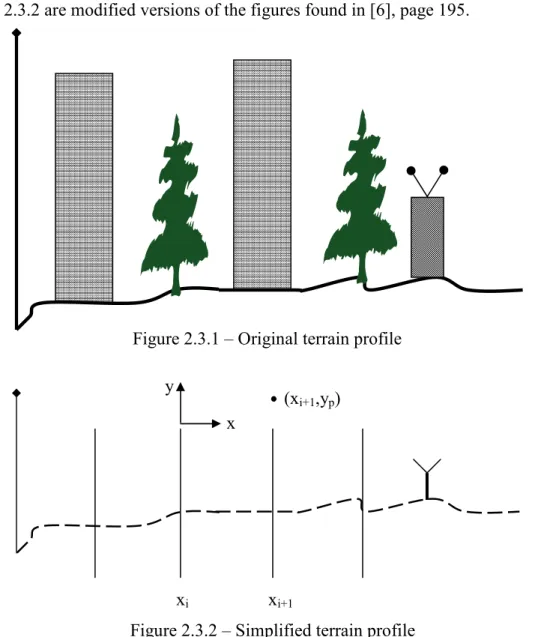
As mentioned earlier the proposed model is based on the half-screen model, where the buildings and trees are replaced by absorbing half-screens. The distance between the screens is a parameter with which the path loss can be changed. The original terrain profile is shown in Figure 2.3.1. The terrain replaced with the half-screens is presented in Figure 2.3.2. Figure 2.3.1 and Figure 2.3.2 are modified versions of the figures found in [6], page 195.

xi xi+1

Figure 2.3.2 – Simplified terrain profile

A wave is propagating from the base station antenna and its amplitude is set to zero behind the screen due to absorption. Then the wave is propagating towards the next absorbing screen with the field above the screen as a form of source. This is repeated along the entire

Figure 2.3.1 – Original terrain profile

x y

(14)

The Helmholtz integral (see Appendix A) should be evaluated in order to determine the diffracted field after an absorbing half-screen. Here, the electric field (E-field) is treated as a complex scalar. The integration along the y-axis is fairly complicated but the Helmholtz integral can be simplified to [6]:

(

+

)

_∫

∞ ⋅ ⋅ ∆ − = 0 ) 2 ( 1 1 ( ) ( , ) 2 , H kr E x y dy r x ik y x E _i _p _i , (2.3.5)

where ∆x=x_i₊₁−x_i is the distance between two neighbouring absorbing screens,

) 2 ( 1

H - the first order Hankel function of the second kind k - the wave number

2

2 ₍ ₎

)

( x y y

r= ∆ + _p − - the distance between the points (x_i,y)and (x_i₊₁,y_p)

When the scalar E-filed E(x_i,y) is known, on and above the preceding half-screen, then with (2.3.5) the scalar E-field on and above the following (next) screen, E(x_i₊₁,y_p) , can be determined for any given position y . _p

To determine the scalar E-field above the first half-screen one can assume a line source, )

exp( 1

ikr

r ⋅ − . Because the calculated result is the field from the line source, then the final field has to be transformed in order to get the corresponding point source field. An approximate method is to multiply the calculated field with

x 1

, where x is the distance between the base station antenna and the mobile antenna. This transformation is only performed at those locations where one wants to determine the final path loss [6].

If we define a function W such that,

(

)

( ) 2 ) 2 ( 1 kr H r x ik y y W _p − = − ∆ ⋅ . (2.3.6)

then expression (2.3.5) can be written in the following way

(

+

)

=

_∫

∞ − ⋅ 0 1,y W(y y) E(x,y)dy x E _i _p _p _i , (2.3.7) or

(

x ₁,y

)

W(y) E(x , y) E _i₊ _p = ∗ _i . (2.3.8)

(15)

Thus, (2.3.7) can be interpreted as a convolution. This means that in order to solve the integral one can determine the Fourier transform of the scalar E-field with respect to y and multiply with the corresponding transformed W-propagator in the k -space: _y

(

,

)

ˆ( ) ˆ( , ) ˆ 1 y y i y i k W k E x k x E ₊ = ⋅ , (2.3.9)

where k is the y-component of _y λ

π 2 =

k .

In order to determine Wˆconsider the wave equation in two dimensions: 0 2 2 2 2 2 = + ∂ ∂ + ∂ ∂ E k x E y E , (2.3.10)

with E(x,y). Fourier transform of (2.3.10) with respect to y yields

₂ˆ ( 2 2)ˆ 0 2 = − + ∂ ∂ E k k x E y , (2.3.11) with E =ˆ Eˆ(x,k_y).

The solution for the one-dimensional Helmholtz equation (2.3.11) is:

( ) 2 2 ) ( ) , ( ˆ i k ky x xi y y C k e k x E = − − − . (2.3.12)

For k_y2 >k2 the branch cut in equation (2.3.12) can be defined as follows,

) ( ) ( ) ( ) ( 2 2 2 2 2 2 2 ) ( ) ( ) ( ) , ( ˆ y i y i ky k x xi y x x k k i y x x k k i y y C k e C k e C k e k x E = − − − − = − − = − − − . (2.3.13)

The constant C is defined when x =x_i

) , ( ˆ ) (k_y E x_i k_y C = , (2.3.14)

and the solution for (2.3.11) can be written as

) ( 2 2 ) , ( ˆ ) , ( ˆ i k ky x xi y i y E x k e k x E = − − − . (2.3.15)

The scalar E-field at x_i₊₁ can be determined by calculating the inverse Fourier transform of the Eˆ -field. A Fast Fourier Transform (FFT) can be used in order to perform the Discrete Fourier Transform (DFT). Using FFT instead of solving the integral directly reduces the computation time considerably.

(16)

3. SIMULATION

3.1 THE HATA MODEL

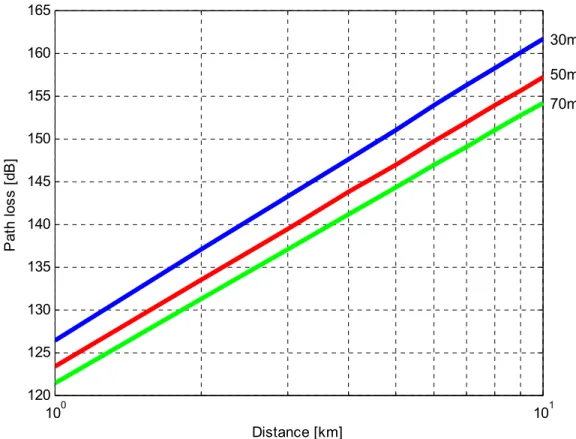
The path loss in an urban area is calculated with the use of the Hata model for the base station antenna heights H = 30m, 50m, 70m and the result is shown in the figure below. The carrier frequency in this case is equal to 900 MHZ and the mobile antenna height is 1.5 m.

100 101 120 125 130 135 140 145 150 155 160 165 Distance [km] P a th l o s s [ d B ]

Figure 3.1.1 –The path loss in an urban area according to the Hata model.

Figure 3.1.2 shows the path loss in a suburban area at the same frequency as above and for the same heights of base antenna and mobile antenna.

30m 50m 70m

(17)

100 101 110 115 120 125 130 135 140 145 150 155 Distance [km] P a th l o s s [ d B ]

Figure 3.1.2 - The path loss in a suburban area according to the Hata model.

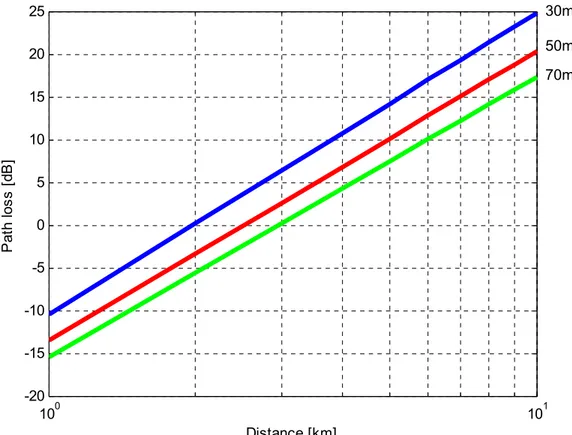
In an open rural area one finds that the loss is considerably smaller, see Figure 3.1.3. The conditions are the same as for the previous cases.

30m 50m 70m

(18)

100 101 -20 -15 -10 -5 0 5 10 15 20 25 Distance [km] P a th l o s s [ d B ]

Figure 3.1.3 - The path loss in an open rural area according to the Hata model.

If the frequency is varied instead one obtains the results shown in Figure 3.1.4. Here, the base station antenna height is chosen to be 70m and the mobile antenna height is 1.5 m. The MATLAB code for the Hata model simulation is presented in Appendix B.

30m 50m 70m

(19)

100 101 110 115 120 125 130 135 140 145 150 155 160 Distance [km] P a th l o s s [ d B ]

Figure 3.1.4 - The path loss in an urban area for the frequencies 450 MHz, 900 MHz, 1500MHz.

3.2 AN FFT BASED MODEL

For an FFT based model the base station antenna height is chosen to be H=50 m, the mobile antenna height h=1.5 m and the height of the buildings G=15 m (the height of the screens). The definitions of the model parameters are given in Figure 3.2.1, which is a modified version of the figure found in [6], page 196.

The main parameters in the model are the distance between the screens w and the distance w′ between the mobile antenna and the nearest screen. A reduction of the distance w leads to an increase in the resulting path loss. The same is valid for the parameter w′.

1500 MHz 900 MHz

(20)

Figure 3.2.1 – Notation for the model parameters.

In the FFT simulation the following data was used: - the carrier frequency fc =900MHz

- the spatial resolution in the vertical y-direction

3 λ = ∆y .

The path loss versus the distance between the transmitter and the receiver (S ∆⋅ x) for the FFT-model with 100 screens is shown in Figure 3.2.2. The distance between screens is equal to 100m and the total distance for the profile is then 10 km. The distance between the mobile antenna and the nearest screen is w′=15 m.

103 104 115 120 125 130 135 140 145 150 155 160 Distance [m] P a th l o s s [ d B ]

(21)

For verification it is useful to compare the FFT-model to an empirical propagation model, for instance the Hata model. The comparison is presented in the next subsection. The code for the FFT-model is developed in MATLAB and given in Appendix C.

3.3 COMPARISON OF THE SIMULATION RESULTS FOR THE HATA MODEL AND THE FFT BASED MODEL

The figures below present a comparison between the propagation loss computed by means of the Hata model and the FFT-model, respectively. The propagation loss is plotted versus the distance between base antenna and mobile antenna (S ∆⋅ x). In Figure 3.3.1 the distance between screens is ∆x=100m and the distance between the mobile antenna and the nearest screen w′=15 m. The carrier frequency is 900 MHz. The base station antenna height, the mobile antenna height and the height of the buildings are the same as in a previous experiment, i.e. H=50 m, h=1.5 m and G=15 m. 103 104 100 110 120 130 140 150 160 170 Distance [m] P a th l o s s [ d B ]

Figure 3.3.1 – Path loss according to the Hata model (dashed line) and the FFT-model (solid line) with ∆x=100 m.

(22)

The oscillations of the FFT result as well as the absolute level of the path loss depend on the distance between screens. Thus, reducing ∆ down to 50 leads to more oscillations and to a x higher path loss, as shown in Figure 3.3.2.

103 104 100 110 120 130 140 150 160 170 Distance [m] P a th l o s s [ d B ]

Figure 3.3.2 – Path loss according to the Hata model (dashed line) and the FFT-model (solid line) with ∆x=50m.

Increasing ∆ up to 125 m produces an FFT result with almost no oscillations and a lower path x loss, as shown in Figure 3.3.3.

(23)

103 104 100 110 120 130 140 150 160 170 Distance [m] P a th l o s s [ d B ]

Figure 3.3.3 – Path loss according to the Hata model (dashed line) and the FFT-model (solid line) with ∆x=125 m.

From the figures above it is obvious that the propagation loss slope of the FFT-model is nearly the same as the slope of the Hata model, which means that the FFT-model can be used to predict the propagation loss due to multiple diffraction.

(24)

4. CONCLUSION

The implementation of the FFT-model with multiple screens gives reasonable agreement with the Hata model. This is verified numerically using MATLAB. The FFT method is numerically efficient and also applicable to the cases where the Hata model is not valid, such as equal antenna and building heights.

After performing different experiments, one finds that the shorter the distance between the screens is, the higher the computed path loss becomes. Moreover, the ripple that appears in the numerical results is reduced when the distance between screens is increased.

Consequently, wave propagation along a terrain profile can be treated as multiple diffraction from absorbing half-screens and can be predicted with fair accuracy by means of the FFT half-screen model.

A problem with the method is the heuristic choice of the model parameters and that numerical convergence in the conventional sense cannot be separated from the actual modelling.

(25)

REFERENCES

[1] J.D. Parsons, The Mobile Radio Propagation Channel, Second Edition. John Wiley & Sons Ltd, 2000.

[2] M. Hata, “Empirical Formula for Propagation Loss in Land Mobile Radio Services”, IEEE VT, 29, p. 317-325, 1980.

[3] H. Holmquist, A DFT Half-Screen Propagation Model for Macrocellular Environments, Master’s thesis, The Royal Institute of Technology, Sweden, 1992.

[4] T.S. Rappaport, Wireless Communications. Principles and Practice, Second Edition. Prentice Hall PTR, 2002.

[5] L. Ahlin, J. Zander and B. Slimane, Principles of Wireless Communications, Third Edition. Studentlitteratur, 2006.

[6] J-E. Berg and H. Holmquist, “An FFT Multiple Half-Screen Diffraction Model”, IEEE VT, 1, p. 195-199, 1994.

(26)

APPENDIX A

The Helmholtz Integral The wave equation:

0

2

2 ₊ ₌

∇ E k E . (A.1)

The Helmholtz integral, which gives the solution for the wave equation is shown below

∫

      ∂ ∂ − ∂ ∂ = − − S ikr ikr dS n E r e r e n E P E

π

4 1 ) ( . (A.2)

For the derivation of the Helmholtz integral (A.2) from Green’s theorem [3] ψ has been chosen equal to

r e−ikr

, where r is the distance from a fixed point P to a variable point P′, both inside the volume

ν

. However, the same result could have been obtained if one would choose

ξ ψ = + − r e ikr , (A.3)

where ξ has no singularities inside and on surface S. Hence, by use of this extended ψ function, (A.2) can be formulated as

∫

      ∂ ∂       + −       + ∂ ∂ = − − S ikr ikr dS n E r e r e n E P E

ξ

π

4 1 ) ( , (A.4)

where ∇2

ξ

+k2

ξ

=0 inside and on S. Suppose, that there is a function

ξ

₁ such that 0 1 = + −

ξ

r e ikr , (A.5)

in every point on S. Then (A.4) can be written as

∫

      + ∂ ∂ = − S ikr dS r e n E P E ₁ 4 1 ) (

ξ

π

. (A.6)

This is an important result as E(P) can be computed by knowing E on S only. Below

ξ

₁ is determined for a plane surface.

(27)

The Rayleigh Integral

Choose for closed surface S the plane Sp, equal to x=0, and a hemi-sphere Shsp with radius R in

the upper half space (x>0). For this special choice of S expression (A.6) may be written as

∫

_∂∂ _ + _ + _∂∂ _ + _ = − − hsp p S ikr S ikr dS r e n E dS r e n E P E ₁ ₁ 4 1 4 1 ) (

ξ

π

ξ

π

. (A.7)

Assume that the electric field E in the upper half space (x>0) is generated by causal sources in the lower half space (x<0), and that one wishes to compute E(P), the electric field E in a point

) , , (y_p z_p x_p

P = corresponding to r=(y_p −y, z_p −z, x_p −x) in the upper half space. Then, for a finite time interval, say 0≤t ≤T_max, R can always be chosen such that the contribution from Shsp

has not yet reached point P for times smaller than T_max . Hence, for a given T_max one can define the radius R =₀ cT_max such that one may take

0 4 1 1 =      + ∂ ∂

∫

Shsp − ikr dS r e n E

ξ

π

. (A.8)

for any R >R₀. Consequently, if one want to know E(P) for t <T_max, expression (A.7) may be replaced by

∫

      + ∂ ∂ = − p S ikr dS r e n E P E ₁ 4 1 ) (

ξ

π

for R >cTmax. (A.9)

The function

ξ

₁ has to be determined such that 0

1 2 1

2 ₊ ₌

∇

ξ

k

ξ

inside and on Sp, (A.10)

and 0 1 = + −

ξ

r e ikr on Sp. (A.11) If r e ikr ′ = ′ − 1

ξ

is chosen with r′=(−x_p −x, y_p −y, z_p −z) then

ξ

₁ satisfies (A.10). Keeping in mind that r =′ r on Sp, it can be seen directly that (A.11) is satisfied as well. Consequently, (A.9)

can be rewritten as dS e e E P E r ik ikr

∫

_∂∂  − _′  = ′ − −

π

1 ) ( ,

(28)

or, using n r r n ∂ ∂ ∂ ∂ = ∂ ∂ and n r r n ∂ ′ ∂ ′ ∂ ∂ = ∂ ∂ :

∫

−       ∂ ′ ∂ − ∂ ∂ + − = p S ikr_dS e n r n r r ikr E P E 2 1 4 1 ) ( π . (A.12)

From the definitions of r and r′

2 2 2 ) ( ) ( ) (x x y y z z r = _p − + _p − + _p − , 2 2 2 ) ( ) ( ) ( x x y y z z r′= − _p − + _p − + _p − .

The gradient of these expressions

φ cos − = ⋅ − = ⋅ ∇ ≡ ∂ ∂ n e n r n r r , (A.13) φ′ − = ⋅ − = ⋅ ′ ∇ ≡ ∂ ′ ∂ ′ n cos e n r n r r , (A.14)

where e_r is the unit vector in the r direction and cosφ = x_p/r. However, the definition of r and r′ states that φ′=π −φ, which implies =cosφ

∂ ′ ∂

n r

. Finally, using the derived expressions in (A.12) the following is obtained

∫

+ − = p S ikr dS e r ikr E P E φ π cos 1 2 1 ) ( 2 . (A.15)

(A.15) is called the Rayleigh integral. It states that any electric field may be synthesized by a dipole distribution on the plane S_p.

For the two-dimensional version of the Rayleigh integral E is independent of z. Then for x=0 (A.15) can be rewritten as

∫

= _

∫

+ _ = − y z l l ikr dy dz e r ikr y x E P E φ π cos 1 ) , 0 ( 2 1 ) ( 2 , (A.16)

or using the first order Hankel function of the second kind,

∫

= − = y l E x y H kr dy ik P E ( 0, )cos ( ) 2 ) ( φ ₁(2) , (A.17) where r = x2_p +(y_p − y)2 .

(29)

APPENDIX B

MATLAB CODE – HATA MODEL Code #1 f_c=900; f_c=900; f_c=900; f_c=900; h_re=1.5; h_re=1.5; h_re=1.5; h_re=1.5; a_re=3.2*( a_re=3.2*( a_re=3.2*(

a_re=3.2*(log10(11.75*h_re))^2log10(11.75*h_re))^2log10(11.75*h_re))^2-log10(11.75*h_re))^2---4.97;4.97;4.97;4.97; d=1:1:10;

d=1:1:10; d=1:1:10;

d=1:1:10; % distances in km% distances in km% distances in km% distances in km h_te=30; h_te=30; h_te=30; h_te=30; Lu_30=69.55+26.16*log10(f_c) Lu_30=69.55+26.16*log10(f_c) Lu_30=69.55+26.16*log10(f_c)

Lu_30=69.55+26.16*log10(f_c)---13.82*log10(h_te)-13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)--a_re+(44.9--a_re+(44.9a_re+(44.9a_re+(44.9---6.55*log10(h_te))*log10(d);-6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d); Lsu_30=Lu_30

Lsu_30=Lu_30 Lsu_30=Lu_30

Lsu_30=Lu_30----2*(log10(f_c/28))^22*(log10(f_c/28))^22*(log10(f_c/28))^22*(log10(f_c/28))^2---5.4;-5.4;5.4;5.4; Lr_30=Lu_30

Lr_30=Lu_30 Lr_30=Lu_30

Lr_30=Lu_30---4.78*(log10(f_c))^2-4.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)-18.33*log10(f_c)--40.98;-40.98;40.98; 40.98; h_te=50; h_te=50; h_te=50; h_te=50; Lu_ Lu_ Lu_

Lu_50=69.55+26.16*log10(f_c)50=69.55+26.16*log10(f_c)50=69.55+26.16*log10(f_c)50=69.55+26.16*log10(f_c)---13.82*log10(h_te)-13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)--a_re+(44.9--a_re+(44.9a_re+(44.9a_re+(44.9---6.55*log10(h_te))*log10(d);-6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d); Lsu_50=Lu_50

Lr_50=Lu_50 Lr_50=Lu_50

Lr_50=Lu_50---4.78*(log10(f_c))^2-4.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)-18.33*log10(f_c)--40.98;-40.98;40.98; 40.98; h_te=70; h_te=70; h_te=70; h_te=70; Lu_70=69.55+26.16*log10(f_c) Lu_70=69.55+26.16*log10(f_c) Lu_70=69.55+26.16*log10(f_c)

Lu_70=69.55+26.16*log10(f_c)---13.82*log10(h_te)-13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)----a_re+(44.9a_re+(44.9-a_re+(44.9a_re+(44.9--6.55*log10(h-6.55*log10(h6.55*log10(h6.55*log10(h_te))*log10(d);_te))*log10(d);_te))*log10(d); _te))*log10(d); Lsu_70=Lu_70

Lr_70=Lu_70 Lr_70=Lu_70

Lr_70=Lu_70---4.78*(log10(f_c))^2-4.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)-18.33*log10(f_c)--40.98;-40.98;40.98; 40.98; % For urban area

% For urban area % For urban area % For urban area figure(1); figure(1); figure(1); figure(1); semilogx(d,Lu_30); semilogx(d,Lu_30); semilogx(d,Lu_30); semilogx(d,Lu_30); hold on hold on hold on hold on semilogx(d,Lu_50,' semilogx(d,Lu_50,' semilogx(d,Lu_50,'

semilogx(d,Lu_50,'----or');or');or'); or'); hold on hold on hold on hold on semilogx(d,Lu_70,'g semilogx(d,Lu_70,'g semilogx(d,Lu_70,'g semilogx(d,Lu_70,'g---*');-*');*');*'); xlabel( xlabel( xlabel(

xlabel('Distance [km]''Distance [km]''Distance [km]''Distance [km]');););); ylabel(

ylabel( ylabel(

ylabel(''''Path loss'Path loss'Path loss'Path loss');););); grid on;

grid on; grid on; grid on;

% For suburban area % For suburban area % For suburban area % For suburban area figure(2); figure(2); figure(2); figure(2); semilogx(d,Lsu_30); semilogx(d,Lsu_30); semilogx(d,Lsu_30); semilogx(d,Lsu_30); hold on hold on hold on hold on semilogx(d,Lsu_50, semilogx(d,Lsu_50, semilogx(d,Lsu_50,

semilogx(d,Lsu_50,''''---or'-or'or'or');); );); hold on hold on hold on hold on semilogx(d,Lsu_70, semilogx(d,Lsu_70, semilogx(d,Lsu_70, semilogx(d,Lsu_70,'g'g'g'g----*'*'*'*');); );); xlabel( xlabel( xlabel(

ylabel( ylabel(

ylabel('Path loss''Path loss''Path loss''Path loss');););); grid on;

% For open rural area % For open rural area % For open rural area % For open rural area figure(3); figure(3); figure(3); figure(3); semilogx(d,Lr_30); semilogx(d,Lr_30); semilogx(d,Lr_30); semilogx(d,Lr_30); hold on hold on hold on hold on semilogx(d,Lr_50, semilogx(d,Lr_50, semilogx(d,Lr_50,

semilogx(d,Lr_50,''''----or'or'or'or');););); hold on hold on hold on hold on semilogx(d,Lr_70, semilogx(d,Lr_70, semilogx(d,Lr_70, semilogx(d,Lr_70,'g'g'g'g---*'-*'*'*');););); xlabel( xlabel( xlabel(

ylabel( ylabel(

ylabel('Path loss''Path loss''Path loss''Path loss');););); grid on;

(30)

Code #2 h_te=70; h_te=70; h_te=70; h_te=70; h_re=1.5; h_re=1.5; h_re=1.5; h_re=1.5; a_re=3.2*(log10(11.75*h_re))^2 a_re=3.2*(log10(11.75*h_re))^2 a_re=3.2*(log10(11.75*h_re))^2 a_re=3.2*(log10(11.75*h_re))^2----4.97;4.97;4.97;4.97; d=1:1:10; d=1:1:10; d=1:1:10;

d=1:1:10; % distances in km% distances in km% distances in km% distances in km f_c=450; f_c=450; f_c=450; f_c=450; Lu_450=69.55+26.16*log10(f_c) Lu_450=69.55+26.16*log10(f_c) Lu_450=69.55+26.16*log10(f_c)

Lu_450=69.55+26.16*log10(f_c)----13.82*l13.82*l13.82*l13.82*log10(h_te)og10(h_te)og10(h_te)og10(h_te)--a_re+(44.9--a_re+(44.9a_re+(44.9-a_re+(44.9---6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d); Lsu_450=Lu_450

Lsu_450=Lu_450 Lsu_450=Lu_450

Lsu_450=Lu_450---2*(log10(f_c/28))^2-2*(log10(f_c/28))^22*(log10(f_c/28))^2-2*(log10(f_c/28))^2---5.4;5.4;5.4;5.4; Lr_450=Lu_450

Lr_450=Lu_450 Lr_450=Lu_450

Lr_450=Lu_450----4.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)18.33*log10(f_c)----40.98;40.98;40.98;40.98; f_c=900; f_c=900; f_c=900; f_c=900; Lu_900=69.55+26.16*log10(f_c) Lu_900=69.55+26.16*log10(f_c) Lu_900=69.55+26.16*log10(f_c)

Lu_900=69.55+26.16*log10(f_c)----13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)--a_re+(44.9--a_re+(44.9a_re+(44.9-a_re+(44.9---6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d); Lsu_900=Lu_9

Lsu_900=Lu_900000000---2*(log10(f_c/28))^2-2*(log10(f_c/28))^22*(log10(f_c/28))^2-2*(log10(f_c/28))^2---5.4;5.4;5.4;5.4; Lr_900=Lu_900

Lr_900=Lu_900 Lr_900=Lu_900

Lr_900=Lu_900----4.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^24.78*(log10(f_c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)18.33*log10(f_c)----40.98;40.98;40.98;40.98; f_c=1500; f_c=1500; f_c=1500; f_c=1500; Lu_1500=69.55+26.16*log10(f_c) Lu_1500=69.55+26.16*log10(f_c) Lu_1500=69.55+26.16*log10(f_c)

Lu_1500=69.55+26.16*log10(f_c)----13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)13.82*log10(h_te)--a_re+(44.9--a_re+(44.9a_re+(44.9-a_re+(44.9---6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d);6.55*log10(h_te))*log10(d); Lsu_1500=Lu_1500

Lsu_1500=Lu_1500 Lsu_1500=Lu_1500

Lr_1500=Lu_1500 Lr_1500=Lu_1500

Lr_1500=Lu_1500---4.78*(log10(f_-4.78*(log10(f_4.78*(log10(f_4.78*(log10(f_c))^2c))^2c))^2c))^2--18.33*log10(f_c)--18.33*log10(f_c)18.33*log10(f_c)-18.33*log10(f_c)--40.98;-40.98;40.98; 40.98; % For urban area

% For urban area % For urban area % For urban area figure(1); figure(1); figure(1); figure(1); semilogx(d,Lu_450); semilogx(d,Lu_450); semilogx(d,Lu_450); semilogx(d,Lu_450); hold on hold on hold on hold on semilogx(d,Lu_900, semilogx(d,Lu_900, semilogx(d,Lu_900,

semilogx(d,Lu_900,''''---or'-or'or'or');); );); hold on hold on hold on hold on semilogx(d,Lu_1500, semilogx(d,Lu_1500, semilogx(d,Lu_1500, semilogx(d,Lu_1500,'g'g-'g'g---*'*'*'*');); );); xlabel( xlabel( xlabel(

ylabel( ylabel(

ylabel('Path loss [dB]''Path loss [dB]''Path loss [dB]''Path loss [dB]');); );); grid on;

% For suburban area % For suburban area % For suburban area % For suburban area figure(2); figure(2); figure(2); figure(2); semilogx(d,Lsu_450 semilogx(d,Lsu_450 semilogx(d,Lsu_450 semilogx(d,Lsu_450);););); hold on hold on hold on hold on semilogx(d,Lsu_900, semilogx(d,Lsu_900, semilogx(d,Lsu_900,

semilogx(d,Lsu_900,''-''---or'or'or'or');); );); hold on hold on hold on hold on semilogx(d,Lsu_1500, semilogx(d,Lsu_1500, semilogx(d,Lsu_1500, semilogx(d,Lsu_1500,'g'g'g'g----*'*'*'*');););); xlabel( xlabel( xlabel(

ylabel( ylabel(

ylabel('Path loss [dB]''Path loss [dB]''Path loss [dB]''Path loss [dB]');); );); grid on;

% For open rural area % For open rural area % For open rural area % For open rural area figure(3); figure(3); figure(3); figure(3); semilogx(d,Lr_450); semilogx(d,Lr_450); semilogx(d,Lr_450); semilogx(d,Lr_450); hold on hold on hold on hold on semilogx(d,Lr_900, semilogx(d,Lr_900, semilogx(d,Lr_900,

semilogx(d,Lr_900,''''---or'-or'or'or');); );); hold on hold on hold on hold on semilogx(d,Lr_1500, semilogx(d,Lr_1500, semilogx(d,Lr_1500, semilogx(d,Lr_1500,'g'g-'g'g---*'*'*'*');); );); xlabel( xlabel( xlabel(

ylabel( ylabel(

ylabel('Path loss [dB]''Path loss [dB]''Path loss [dB]''Path loss [dB]');); );); grid on

grid on grid on grid on

(31)

APPENDIX C

MATLAB CODE – FFT BASED MODEL

clear all; clear all; clear all; clear all; lambda=0.33; lambda=0.33; lambda=0.33; lambda=0.33; delta_x=100; delta_x=100; delta_x=100; delta_x=100; H=50; H=50; H=50; H=50; G=15; G=15; G=15; G=15; max_p=2022; max_p=2022; max_p=2022; max_p=2022; delta_yr=lambda/3; delta_yr=lambda/3; delta_yr=lambda/3; delta_yr=lambda/3; p p p p=37;=37;=37;=37; y_p=0:max_p y_p=0:max_p y_p=0:max_p y_p=0:max_p;;; ; Efield=sqrt(delta_x^2+(y_p Efield=sqrt(delta_x^2+(y_p Efield=sqrt(delta_x^2+(y_p

Efield=sqrt(delta_x^2+(y_p----H).^2*delta_yr^2);H).^2*delta_yr^2);H).^2*delta_yr^2); H).^2*delta_yr^2); Input_Efield=exp(i*2*pi/l

Input_Efield=exp(i*2*pi/l Input_Efield=exp(i*2*pi/l

Input_Efield=exp(i*2*pi/lambda*Efield)./Efield;ambda*Efield)./Efield;ambda*Efield)./Efield;ambda*Efield)./Efield; for y_p = 1:

for y_p = 1: for y_p = 1:

for y_p = 1:max_pmax_pmax_pmax_p+1,+1,+1,+1, if (y_p if (y_p if (y_p if (y_p---1) < G -1) < G 1) < G 1) < G New_Efield(y_p)=0; New_Efield(y_p)=0; New_Efield(y_p)=0; New_Efield(y_p)=0; elseif (y_p elseif (y_p elseif (y_p elseif (y_p---1) > G-1) > G1) > G1) > G New_Efield(y_p)=Input_Efield(y_p); New_Efield(y_p)=Input_Efield(y_p); New_Efield(y_p)=Input_Efield(y_p); New_Efield(y_p)=Input_Efield(y_p); else else else else New_Efield(y_p)=Input_Efield(y_p)*0.5; New_Efield(y_p)=Input_Efield(y_p)*0.5; New_Efield(y_p)=Input_Efield(y_p)*0.5; New_Efield(y_p)=Input_Efield(y_p)*0.5; end end end end end end end end for y_p = 1: for y_p = 1: for y_p = 1:

for y_p = 1:mmmmax_pax_pax_pax_p+1,+1,+1,+1, if (y_p

if (y_p if (y_p

if (y_p---1) > (-1) > (1) > (1) > (mmmmax_pax_pax_p)/2; ax_p)/2; )/2; )/2; temp3(y_p)=(cos((y_p

temp3(y_p)=(cos((y_p temp3(y_p)=(cos((y_p

temp3(y_p)=(cos((y_p---m-mmmax_pax_pax_pax_p*0.5*0.5-*0.5*0.5---1)*pi/(1)*pi/(1)*pi/(1)*pi/(max_pmax_pmax_pmax_p*0.5))+1)/2; *0.5))+1)/2; *0.5))+1)/2; *0.5))+1)/2;

New_Efield(y_p)=New_Efield(y_p)*temp3(y_p); New_Efield(y_p)=New_Efield(y_p)*temp3(y_p); New_Efield(y_p)=New_Efield(y_p)*temp3(y_p); New_Efield(y_p)=New_Efield(y_p)*temp3(y_p); end end end end end end end end CFFT_New_Efield=fft(New_Efield)/( CFFT_New_Efield=fft(New_Efield)/( CFFT_New_Efield=fft(New_Efield)/(

CFFT_New_Efield=fft(New_Efield)/(mmmmax_pax_pax_pax_p+1); +1); +1); +1); for y_p = 1:

for y_p = 1: for y_p = 1:

for y_p = 1:mmmmax_pax_pax_pax_p+1,+1,+1,+1, k_y1(y

k_y1(y k_y1(y

k_y1(y_p)=(y_p_p)=(y_p_p)=(y_p-_p)=(y_p---1)/((1)/((m1)/((1)/((mmax_pmax_pax_pax_p+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi; k_y2(y_p)=((y_p

k_y2(y_p)=((y_p k_y2(y_p)=((y_p

k_y2(y_p)=((y_p--1)--1)1)1)----(((m(max_pmmax_pax_pax_p+1))/((+1))/((+1))/((+1))/((max_pmax_pmax_p+1)*delta_yr)*2*pi;max_p+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi; +1)*delta_yr)*2*pi;

if (y_pif (y_pif (y_pif (y_p---1) < (-1) < (1) < (1) < (max_pmax_pmax_pmax_p)/2; )/2; )/2; )/2; if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2), CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----i*sqrt((2*pi/lami*sqrt((2*pi/lami*sqrt((2*pi/lami*sqrt((2*pi/lambda)^2bda)^2bda)^2bda)^2--- -k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); else else else else CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2--- -(2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); end end end end else else else else if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), CFFT_New_Efield(y_p)=CFFT_New_Efiel CFFT_New_Efield(y_p)=CFFT_New_Efiel CFFT_New_Efield(y_p)=CFFT_New_Efiel

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(d(y_p)*exp(d(y_p)*exp(d(y_p)*exp(----i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2--- -k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); else else else else CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2--- -(2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); end end end end end end end end end end end end ICFFT_New_Efield=ifft(CFFT_New_Efield)*( ICFFT_New_Efield=ifft(CFFT_New_Efield)*( ICFFT_New_Efield=ifft(CFFT_New_Efield)*(

ICFFT_New_Efield=ifft(CFFT_New_Efield)*(mmmax_pmax_pax_p+1); ax_p+1); +1); +1); for s for s for s for ss=1:100,s=1:100,s=1:100,s=1:100,

TotFFTTotFFTTotFFTTotFFT(:,ss)=ICFFT_New_Efield;(:,ss)=ICFFT_New_Efield;(:,ss)=ICFFT_New_Efield; (:,ss)=ICFFT_New_Efield;

for y_p = 1:for y_p = 1:for y_p = 1:for y_p = 1:max_pmax_pmax_pmax_p+1,+1,+1,+1, if (y_p if (y_p if (y_p if (y_p---1) < G -1) < G 1) < G 1) < G New_Efield(y_p)=0; New_Efield(y_p)=0; New_Efield(y_p)=0; New_Efield(y_p)=0; elseif (y_p elseif (y_p elseif (y_p elseif (y_p---1) > G-1) > G1) > G1) > G New_Efield(y_p)=ICFFT_New_Efield(y_p); New_Efield(y_p)=ICFFT_New_Efield(y_p); New_Efield(y_p)=ICFFT_New_Efield(y_p); New_Efield(y_p)=ICFFT_New_Efield(y_p); else else else else New_Efield(y_p)=I New_Efield(y_p)=I New_Efield(y_p)=I

New_Efield(y_p)=ICFFT_New_Efield(y_p)*0.5;CFFT_New_Efield(y_p)*0.5;CFFT_New_Efield(y_p)*0.5;CFFT_New_Efield(y_p)*0.5; end end end end end end end end

(32)

end end end end

CFFT_New_Efield=fft(New_Efield)/( CFFT_New_Efield=fft(New_Efield)/( CFFT_New_Efield=fft(New_Efield)/(

CFFT_New_Efield=fft(New_Efield)/(mmmmax_pax_pax_pax_p+1); +1); +1); +1); for y_p = 1: for y_p = 1: for y_p = 1: for y_p = 1:mmmmax_pax_pax_pax_p+1,+1,+1,+1,

k_y1(y_p)=(y_p k_y1(y_p)=(y_p k_y1(y_p)=(y_p

k_y1(y_p)=(y_p----1)/((1)/((1)/((m1)/((mmax_pmax_pax_pax_p+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi; k_y2(y_p)=((y_p

k_y2(y_p)=((y_p k_y2(y_p)=((y_p

k_y2(y_p)=((y_p--1)--1)1)-1)---(((m(max_pmmax_pax_pax_p+1))/((+1))/((+1))/((+1))/((max_pmax_pmax_p+1)*delta_yr)*2*pi;max_p+1)*delta_yr)*2*pi;+1)*delta_yr)*2*pi; +1)*delta_yr)*2*pi;

if (y_pif (y_pif (y_pif (y_p---1) < (-1) < (1) < (1) < (max_pmax_pmax_pmax_p)/2; )/2; )/2; )/2;

if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2), if (k_y1(y_p)^2<(2*pi/lambda)^2),

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2--- -k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); k_y1(y_p)^2)*delta_x); else else else else CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2sqrt(k_y1(y_p)^2--- -(2*pi/lambda)

(2*pi/lambda) (2*pi/lambda)

(2*pi/lambda)^2)*delta_x);^2)*delta_x);^2)*delta_x);^2)*delta_x); end end end end else else else else if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), if (k_y2(y_p)^2<(2*pi/lambda)^2), CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp( CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(----i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2i*sqrt((2*pi/lambda)^2--- -k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); k_y2(y_p)^2)*delta_x); else else else else CFFT_New_Efield(y_p)=CFFT CFFT_New_Efield(y_p)=CFFT CFFT_New_Efield(y_p)=CFFT

CFFT_New_Efield(y_p)=CFFT_New_Efield(y_p)*exp(_New_Efield(y_p)*exp(_New_Efield(y_p)*exp(-_New_Efield(y_p)*exp(---sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2sqrt(k_y2(y_p)^2--- -(2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); (2*pi/lambda)^2)*delta_x); end end end end end end end end end end end end ICFFT_New_Efield=ifft(CFFT_New_Efield)*( ICFFT_New_Efield=ifft(CFFT_New_Efield)*( ICFFT_New_Efield=ifft(CFFT_New_Efield)*(

ICFFT_New_Efield=ifft(CFFT_New_Efield)*(mmmax_pmax_pax_p+1);ax_p+1);+1); +1); end end end end fo fo fo for S=1:100,r S=1:100,r S=1:100, r S=1:100, tmp2(S)= tmp2(S)= tmp2(S)=

tmp2(S)=----20*log10(abs(20*log10(abs(20*log10(abs(20*log10(abs(TotFFTTotFFT(51,S))/sqrt(S*delta_x))+TotFFTTotFFT(51,S))/sqrt(S*delta_x))+(51,S))/sqrt(S*delta_x))+p(51,S))/sqrt(S*delta_x))+pp;p;;; end

end end end

x=[10:100]*delta_x; x=[10:100]*delta_x; x=[10:100]*delta_x; x=[10:100]*delta_x; AXIS([1000 10000 100 170])AXIS([1000 10000 100 170])AXIS([1000 10000 100 170])AXIS([1000 10000 100 170])

semilogx(x,tmp2(10:100)) semilogx(x,tmp2(10:100)) semilogx(x,tmp2(10:100)) semilogx(x,tmp2(10:100)) grid on;grid on;grid on;grid on;

xlabel(xlabel(xlabel(xlabel('Distance [m]''Distance [m]''Distance [m]''Distance [m]');););); ylabel(ylabel(ylabel(ylabel('Path loss [dB]''Path loss [dB]''Path loss [dB]''Path loss [dB]');); ););