Prime Time in Preschool Through Teacher-Guided Play with Rectangular Numbers

Full Terms & Conditions of access and use can be found at

https://www.tandfonline.com/action/journalInformation?journalCode=csje20

ISSN: (Print) (Online) Journal homepage: https://www.tandfonline.com/loi/csje20

Prime Time in Preschool Through Teacher-Guided

Play with Rectangular Numbers

Jöran Petersson & Kassahun Weldemariam

To cite this article: Jöran Petersson & Kassahun Weldemariam (2021): Prime Time in Preschool Through Teacher-Guided Play with Rectangular Numbers, Scandinavian Journal of Educational Research, DOI: 10.1080/00313831.2021.1910561

To link to this article: https://doi.org/10.1080/00313831.2021.1910561

© 2021 The Author(s). Published by Informa UK Limited, trading as Taylor & Francis Group

Published online: 08 Apr 2021.

Submit your article to this journal

View related articles

Prime Time in Preschool Through Teacher-Guided Play with

Rectangular Numbers

Jöran Petersson aand Kassahun Weldemariam b

a

Malmö University, Sweden;bUniversity of Gothenburg, Sweden

ABSTRACT

In preschool, numbers and shapes typically appear as separate topics. This study explores how a game, designed as a guided play activity with figurate numbers, functions in a preschool context. The guided play involved parking Lego cars in a rectangular shape, and tofind out for which number of Lego cars this is possible. Thirteen preschool children in three separate age groups, aged from four to six years, together with their teacher, participated in the study. Their communications through words and actions were recorded. The results exemplify how this guided play provides a rich context for engaging young children with mathematical activities such as counting, sorting, shaping, asking, justifying, and inferring, as well as emotional engagement with the activity.

ARTICLE HISTORY

Received 17 August 2020 Accepted 24 March 2021

KEYWORDS

Figurate numbers; guided play; mathematics; number patterns; pedagogy of play; preschool

Introduction

Conventionally, numbers and shapes appear as separate topics in preschool, with not much com-monality found between them (see, e.g., Saracho & Spodek,2009). The mathematical discipline of figurate numbers, however, connects numbers and shapes, and is not insignificant in mathematics. Historically, it has been an important inspiration to research in mathematics, from the Pythagorean tradition to Pascal, and later on a source for recreational mathematics (Gardner,2001). Related to figurate numbers is geometric algebra, which in mathematics education has a wide range of appli-cations, such as multiplying and factoring arithmetic and algebraic expressions, solving quadratic equations, and working out number sequences whilst, at the same time, making these ideas visual (Suzuki, 2009). Young children’s mathematical abilities with respect to numbers, shapes, and

reasoning (Charlesworth,2005; Clements et al.,1999; English,1991), together with the recreational and visual potential forfigurate numbers, suggest the following aim for this article: To explore the mathematical content in a preschool activity designed as guided play with rectangular numbers in the context of parking Lego cars on a road ferry.

Figurate and Rectangular Numbers in Mathematics Teaching

The idea offigurate numbers has ancient roots. Early numeral systems such as the Babylonian and Egyptian (about 2000 BC) wrote numbers as rectangular patterns of dots or lines in groups of two or three (Katz,1998). For example, in the early Babylonian numeral system, the number nine is a rectangular three by three pattern and in the early Egyptian numeral system, the number eight is

© 2021 The Author(s). Published by Informa UK Limited, trading as Taylor & Francis Group

This is an Open Access article distributed under the terms of the Creative Commons Attribution-NonCommercial-NoDerivatives License (http:// creativecommons.org/licenses/by-nc-nd/4.0/), which permits non-commercial re-use, distribution, and reproduction in any medium, provided the original work is properly cited, and is not altered, transformed, or built upon in any way.

CONTACT Jöran Petersson joran.petersson@mau.se https://doi.org/10.1080/00313831.2021.1910561

a rectangular two by four pattern. By combining the concepts of shape and cardinality into“number shapes”, the Pythagorean tradition developed the idea of figurate numbers into a mathematically fruitful discipline of its own. The idea offigurate numbers has proven useful not only within the history of mathematics but also in present mathematics education because it provides a concrete and multi-modal way to represent both numbers and several important mathematical ideas.

Steinbring (1997), for example, compares two ways of representing arithmetic situations for pri-mary school children. When representing the arithmetic situation with digits only, the children demonstrated difficulties in understanding the highlighted mathematical principles and developed procedural knowledge instead. When representing the arithmetic situation with digits and as rec-tangular numbers on a 100-dotfield for visualising multiplication situations, the children demon-strated significantly more meaning-making, reasoning, and knowledge. In a similar manner, rectangular numbers have proven supportive for meaning-making in multiplication situations and properties of multiplication in primary school (Barmby et al.,2009; Bolden et al.,2013; Larsson et al.,2017). Moreover, visual representations of numerical magnitude support children’s learning of arithmetic (Booth & Siegler,2008). In addition, Bertelli et al. (1998) found that using concrete operations helped children aged three to four year solve arithmetic tasks involving numbers larger than the children were expected to be able to count to. In summary, learning to move between different representational forms is important; indeed, following a survey of the literature, Andrews and Sayers (2015) conclude that one aspect of developing number sense for children in early school years is to know that numbers have different representational forms. Duval (2006, p. 128) even states that,“The true challenge of mathematics education is first to develop the ability to change representation register.”

In terms of representational forms, working withfigurate numbers includes moving back and forth between symbolic representations, such as numbers, and iconic representations, such as pic-torial or geometric objects. In contrast, working with patterns often restricts learners either to ico-nic representations, such as geometrical patterns, or to symbolic representations, such as the number sequence 1-2-1-2. Vogel (2005) suggests using pattern activities such as identifying, extend-ing, reproducextend-ing, comparing and describing patterns as a means of learning to think mathemat-ically and, later on, using them for modelling real-life situations. Tiling a rectangular space on a piece of paper by drawing and counting the squares, for example, might be an advanced task for early primary school students (Battista et al.,1998). Preschool children might even be able to do this on their own initiative (Fox,2005), though the more common case is that this is a teacher-initiated activity. For example, preschool children were, at different achievement levels, able to reproduce and complete graphic patterns such as a hopscotch pattern or an ABAB-pattern of digits or colours (Papic et al.,2011). In primary school, one common function of patterns is to support the teaching of counting, arithmetic and algebraic structures, geometry, and data exploration (Clem-ents & Sarama,2011; Cross et al.,2012; Fox,2005; Papic,2007; Vogel,2005).

Young Children Identifying Shapes

In research literature on young children learning shapes, the circle, rectangle, square and triangle are often mentioned (Clements & Sarama,2007). Of these shapes, the rectangle seems the easiest to grasp. For example, Elia and Gagatsis (2003) found that young children showed moreflexibility in working with rectangles than with other polygons as they varied the size of one or two dimensions of the polygons, and Shiakalli (2014) explored preschool children’s mathematical activity during a task involving constructing squares with different sizes. Clements et al. (1999) provide a third example, taken from the results of clinical interviews with children aged approximately 4–7 years. In their study, the children were asked to select the rectangles from among given quadrilateral shapes. The children preferred shapes that were“long” and had at least one pair of opposite parallel sides, which, however, included some non-rectangular parallelograms and trapezoids. Moreover, they found that young children were not only able to see similarities between one shape and a

prototype shape but also to make declarative statements and thus give descriptive arguments for classifying a shape as, for example, a rectangle. In their study, there were only small differences in achievement on classifying rectangles between children of different ages. Since, for young chil-dren, rectangles seem easier to recognize than other shapes, it is likely that rectangular numbers are less difficult to recognize than other figurate numbers.

Young Children’s Quantifying

Habituation and dishabituation experiments have shown that infants possess early numeracy abilities. For example, Antell and Keating (1983) showed that children younger than one week could dis-tinguish between 2 and 3 dots (but not between 4 and 6 dots) shown on different pictures. A more advanced version of this experiment is to observe children’s reaction to putting two identical objects behind a curtain, then removing the curtain and only one object being visible, thus corre-sponding to the incorrect arithmetic statement 1 + 1 = 1. Five-month-old children could distinguish between this incorrect arithmetic statement and the correct one 1 + 1 = 2 (Wynn,1992). Hence, chil-dren develop the ability to count very early and, accordingly, several test instruments for evaluating both mathematical content in preschool activities and mathematical knowledge of children have a main focus on counting, number symbols, sorting, and early arithmetic (Charlesworth & Leali,

2012; Clements & Sarama,2007; Kilday & Kinzie,2009; Van de Rijt et al.,1999; Warfield,2001). In addition, numbers can also be used for the purpose of learning to reason using numbers, and for exploring properties of numbers themselves. Besides counting and doing operations on num-bers, young children are also capable of conducting mathematical work strategically and systema-tically. For example, English (1991) let children aged 4–11 years solve combinatorial problems. In some cases, children as young as four years old showed the beginning of systematic search and some seven-year-old children showed advanced combinatorial solving strategies and could provide argu-ments for their conclusions.

Guided Play

Play and learning are believed to be inseparable entities in young children’s everyday life (Pramling Samuelsson & Johansson, 2006; Van Oers, 2010), including mathematics learning in preschool (Björklund et al.,2018; Reikerås,2020). Hence, it makes sense to develop a pedagogy of play that clar-ifies the teacher’s role in this learning. Accordingly, Edwards and Cutter-Mackenzie (2011), Pramling Samuelsson and Asplund Carlsson (2008), and Stephen (2010) distinguished between free, guided

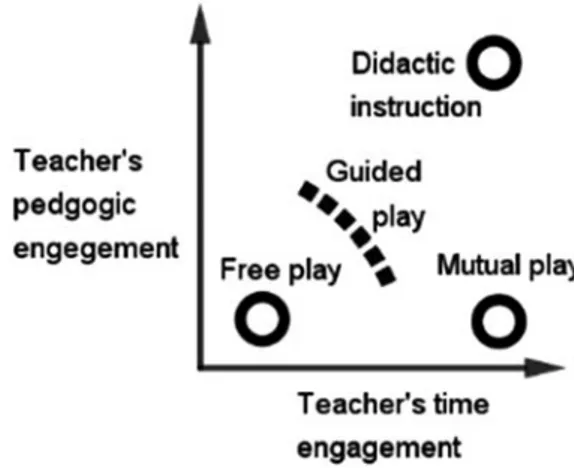
(also called structured) and mutual play in which the teacher engages in the children’s play for differ-ent periods of time, as illustrated inFigure 1. One example of mutual play is board games, which Ramani and Siegler (2008) found benefitted number learning, particularly when the games involved a number track. Hence, mutual play could constitute a learning opportunity without intended ped-agogical engagement. Along the dimension of the teacher’s pedagogical engagement, Fisher et al. (2013) compared free play, guided play, and didactic instruction with respect to preschoolers’ learn-ing. In a confirmative experiment, with one child at a time, they found guided play to be the most and free play the least effective with respect to the children’s learning outcomes.

Figure 1illustrates that guided play performs an intermediate role when compared with free play, mutual play, and didactic instruction with respect to the teacher’s synchronous engagement with the children. Guided play requires the teacher’s engagement as a supporter and facilitator of children’s learning, but without taking away the children’s authority to lead, control, and regulate their play (Björklund et al.,2020; Pramling Samuelsson & Asplund Carlsson,2008; Stephen,2010; Synodi,2010). Guided play is a commonly employed strategy for preschool and pre-primary tea-chers as they frame mathematical learning opportunities for the children (Björklund, 2015). In addition, teachers are expected to be creative and to embed mathematical skills within everyday free and structured play at preschool (Cutter-Mackenzie et al., 2014). One type of guided play, as indicated by Edwards and Cutter-Mackenzie (2011), is a purposefully framed game whereby a teacher sets the structure and provides the children with materials and playful activities and instruc-tions that entail concepts. Two examples of this approach in Swedish preschool are described by Doverborg and Pramling-Samuelsson (2000) and Ekdahl (2020).

Research Question

Figurate numbers, a number of concrete objects shaped in some pattern, has been a powerful tool in mathematics history and useful in mathematics education at various school levels. However, research into usingfigurate numbers as a visual tool for exploring various properties of numbers seems sparse for young children and, in particular, for preschool children. With the aim of adding a piece of knowledge to address this gap, the present study sets out to answer the following research question: How does a preschool game function, when designed as guided play withfigurate num-bers? This guided play involves a game whereby children try to park a given number of Lego cars in a rectangular shape on a road ferry. Accordingly, the focus is essentially on the participating chil-dren’s engagement and mathematical initiatives during the game but also the teacher’s role in monitoring the children’s game.

Method

The research question consists of three intertwined aspects. First, the designed task is a game, and a methodological choice was to explore it as a single experiment case study preceded by a pilot study. Second, the actual data are the children’s play during this game, which was audio-videorecorded. Third, these recordings were analysed with respect to the engagement and mathematical content in the children’s play and the teacher’s role in the communication. As this is a design study, its focus is confined to how the game on rectangular numbers works in preschool with respect to the engagement and mathematical activities it creates in the group, and does not include the chil-dren’s individual short-term or long-term learning.

Designing and Piloting the Explored Game

As indicated above, this study explores a snapshot of a mathematical game purposefully designed for preschool children. In this game, designed as guided play, the teacher provided material for the children as well as playful activities suggestive of concepts, mathematical ones in this case (Edwards

& Cutter-Mackenzie,2011). The materials used in this guided play are identically-sized Lego cars and cardboard road ferries, as shown inFigure 2.

The activity involved parking the Lego cars in a rectangular pattern on the road ferries and, as such, concerned working with patterns, as in Elia and Gagatsis (2003), Fox (2005), Papic (2007), Shiakalli (2014), and Vogel (2005). The ferries were cut out in different widths to make space for different numbers of parking columns (2, 3 and 5 columns) to be drawn on them matching the width of the Lego cars. The children were given one road ferry and a specified number of Lego cars and were asked to ascertain whether it was possible to park the cars in a rectangular shape on the ferry. One parking rule in the activity was that all parking columns on the road ferry must be used in order to make sure it could balance on the water. A second parking rule was that the cars must be parked within the marked-out parking columns on the road ferry since this is the way cars drive on and off on real road ferries. Whilst the children played the game, the teacher took the guided play role of reminding the children of these rules.

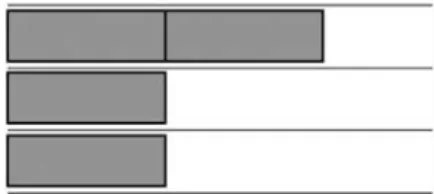
When the children indicated that they were done with parking the cars, the teacher asked if the cars were parked in a rectangular shape. The teacher’s guided play role was then to ask the children to count how many cars they had parked and tofind a flash card with that number on it. Each flash card had a number on it, from 3 to 10. Finally, the teacher asked the children to sort their numbers into rectangular or non-rectangular numbers and to place theirflash cards on one of two papers marked“Yes, a rectangular number” and “No, a non-rectangular number” (seeFigure 2).

The present study was piloted with an activity similar to the one described above. Instead of Lego cars and ferries, a number of A4 pieces of paper were used as concrete objects and the children in the pilot experiment were three to four years old. The pilot experiment went well with the four-year-old children while some of the three-four-year-old children had difficulty counting and expressing their ideas in words. To obtain fruitful data from the experiment, age was considered, and the chil-dren were chosen to be four years and older. Both the pilot study and the game of parking Lego cars on a road ferry are adapted versions of the“sieve of Eratosthenes” (Katz,1998) as a way to dis-tinguish between rectangular numbers (numbers occurring in a multiplication table; composite numbers) and non-rectangular numbers (prime numbers). In short, the design of this game

followed the research of Habgood and Ainsworth (2011), who suggested a game development design prioritizing, first, the learning content (rectangular number), then the game mechanics (Lego cars and cardboard ferries), and,finally, a fantasy context (parking cars on a road ferry).

Collecting Data

The participants in the study were preschool children aged 4–6 and, for the oldest children, this was their last semester in preschool. The participating teacher is a licensed preschool teacher, who received instructions about how to play the game. The outcome of the pilot study suggested four years old as a minimum suitable age for this game. Although it was not the intention of the study to evaluate the children’s knowledge of numerals and number symbols, the participating chil-dren’s teacher checked this because it was a prerequisite of the game. All participating children were able to count at least 10 objects and to recognize number symbols from 1 to 10, and the tasks involved in the study were within their knowledge limit. Moreover, the children’s knowledge about rectangular shapes was sufficient for the present study; they could identify them as quadri-corners or quadrilaterals with two long opposite sides, as did the children in Clements et al. (1999). Preschool children experience significant cognitive development as they grow from four

to six years old. For this reason, the researchers chose a preschool with age-divided groups, Alliga-tors, Caymans, and Crocodiles (see Table 1). Alligators were the youngest group, with children approximately four years old; Caymans were aged aboutfive, and Crocodiles were about six. The game was played with one group at a time on different days.

Various scholars emphasize the purposefulness of actions in children’s communication. For example, Bertelli et al. (1998) and Norris (2002) indicate how actions carry meaning during social interplay. For this reason, the children’s play was audio-videorecorded. To ensure good-quality audio-recordings, separate Dictaphones were placed on thefloor to record the voices. Two video cameras were set at different angles. One video camera filmed the children’s facial and emotional expressions and the other, angled downwards, filmed the floor where the children’s hands-on actions were playing out (see e.g., Häikkilä & Sahlström, 2003). Hence, the data consist of both actions and verbal and emotional expressions of the children and their teacher.

This study followed the ethical standards of the Swedish central ethical review board for exper-iments involving human participants (Hermerén,2011). Parents and the preschool (principal and teachers) got information about the study. Elected as participants were those children whose parents had given written consent. The children’s willingness was also taken into consideration during the experiment. While the guided play activity was going on, the children were set free to join in and withdraw from the play at any time during the experiment. Each group of children spent about 20 minutes on the activity.

Table 1.Participating preschoolers.

Group (pseudonyms) Child (pseudonyms) Age (years:months)

Alligators Harold 4:10 Monique 4:3 Youssef 4:5 Caymans Adam 5:6 Nicholas 5:6 Victor 5:5 Wilma 5:11 Crocodiles Douglas 5:11 Esmeralda 5:3 Gertrude 5:10 Marcus 5:10 Noel 6:3 Zahra 5:11

Analysing Data

Cognitive and emotional aspects have both been shown to be important elements of building atti-tudes to learning mathematics (Hannula,2002,2012). For the preschool context, the cognitive and emotional aspects are important in guided play since the cognitive aspect is crucial in the “peda-gogy” and the emotional aspect is crucial in the “guided play”. The recorded audio-video data was analysed with respect to the communication in words and actions during the game. Along with the research question, the children’s and the teacher’s mathematical communication was cate-gorized as a cognitive aspect and the children’s engagement was categorized as an emotional aspect when they displayed obvious emotional reactions.

Viewing the audio-video material as a narrative, the researchers analysed its plot structure with respect to narrative elements that were important in constituting the mathematical milieu during the designed game. Narrative elements induced through the design of the task and initiated by the teacher were: presenting the road ferry context; parking cars in rectangular patterns; and decid-ing whether a number was rectangular or non-rectangular; teacher interventions were in the form of guiding prompts, questions, and acts. Narrative elements categorized as the children’s emotional engagement with the game were exclamations, pitch, and gestures. Narrative elements categorized as the children’s cognitive engagement with the game and initiated by the children were self-cor-recting of infeasible solutions; taking teacher-independent mathematical initiatives; and handling the number nine, which participants found difficult. Both authors agreed on these identified narratives.

Results

Introducing the Road Ferry Context

The teacher introduced the activity by showing photographs of real road ferries that serve as float-ing bridges, transportfloat-ing vehicles between islands in the archipelago. The purpose of the introduc-tion was to familiarize the children with the context and to make it a concrete applicaintroduc-tion that concerns everyday life, thus making it seem a practical problem that could have relevance for every-day living. It also made sense of the two parking rules: along the columns and in all columns.

The teacher started by showing one picture of a road ferry with three parking columns and cars in all columns. Some children seemed familiar with this context since they related it to their real-life experience and mentioned that they had, or had not, seen road ferries before. In response to thefirst picture, Victor in Caymans commented:“This is a car boat.” In the youngest group (Alligators), two children spontaneously commented:

. I went there. (Youssef in Alligators)

. No, I didn’t. (Harold in Alligators, responding to Youssef)

Next, the teacher showed a picture of another road ferry and asked the children to count the number of parking columns. Harold in Alligators correctly counted the parking columns tofive. No children in the older groups experienced problems counting the parking columns. Harold’s counting of the parking columns in one of the road ferries shows that he was comfortable with the context, despite having no personal experience of road ferries.

Parking Cars in Rectangular Shapes

After having introduced the road ferry context using pictures, the teacher introduced the concrete materials for the game. In the Alligators group, the teacher introduced a cardboard road ferry with two parking columns and asked the children to park two Lego cars on it. The teacher gave the chil-dren one more Lego car at a time as the chilchil-dren asked for more. The teacher asked,“Can we park

two cars on the ferry so that they can make a rectangle shape together?” Harold drove two Lego cars on board while making a car sound, “ooon”, demonstrating immersive engagement common in play activities, while Youssef watched carefully. Youssef adjusted the position of the two cars a little bit so that they made a proper rectangle. The teacher handed out a third car and Harold drove it on-board and said,“We need one more”. The teacher encouraged the children to take a fourth Lego car. When Harold had parked it, the teacher asked if the cars were parked in a rectangular shape. Harold nodded and said,“Yes.” The teacher gave a fifth car to Harold and asked, “Can we park a fifth car so that it makes a rectangle?” Harold drove the car on-board with an accompanying sound, “ooon”. Whilst he was doing so, Youssef said,“We need one more car”, stretched for one and parked it so that it completed a rectangular shape. The teacher then asked the children to show how they knew that the shape was a rectangle. Harold pointed at each of the four corners as he counted them aloud,“One, two, three, four.”

The activity went on in a similar manner up to 10 cars. By their responses to the task, the two young children in Alligators showed that they understood the concept of parking Lego cars in a rectangular shape. For example, Youssef, in the excerpt above, said, “We need one more car.” Later, when Alligators worked with a ferry with three parking columns and had parked four cars, as shown inFigure 3, Harold said“we need two more cars”. Youssef and Harold thus showed that they knew how to park the cars in a rectangular shape and how many cars were required tofill up the empty spaces in order to make a rectangle.

Distinguishing Numbers as Rectangular or Non-Rectangular

Once the children were familiar with parking the Lego cars in a rectangular pattern, the teacher introducedflash cards marked with a number and the two papers with the text “Yes, a rectangular number” and “No, a non-rectangular number” (seeFigure 2). In the Caymans and Crocodiles, the teacher asked if the children could help read the text:

. … No … a … . (Adam from Caymans started)

. No, a… non … rect … rectangular number. (Victor from Caymans took over from Adam and continued)

The teacher parked three Lego cars on the road ferry with two columns, as shown inFigure 4, and asked the children if they could park the third car somewhere else to make a rectangular shape. Adam replied,“No” to this question from the teacher.

Subsequently, the teacher brought out the numberedflash cards and asked if they should put the flash card marked with number “three” on the paper marked “Yes, a rectangular number” or on the paper marked“No, a non-rectangular number”. All Cayman group children responded in chorus, “No”, and Wilma pointed at the paper marked “No, a non-rectangular number”. The teacher gave a fourth car to the children. Victor arranged the four cars in a two by two pattern and that was fol-lowed by a whispering“Yeah!” from Adam. Victor pointed to the paper marked “Yes, a rectangular number” and said “four can go to the green one”, since that paper had a green check box on it. After

a while, the children in the Caymans group were positively competing tofind the numbered flash card in question and put it on the appropriate paper marked“Yes” and “No”, respectively.

In summary, in all three groups (Alligators, Caymans, Crocodiles), the children were able to recognize whether or not the cars were parked in a rectangular shape, to count the number of Lego cars, and to correctly put each corresponding numbered flash card on one of the papers marked“Yes, a rectangular number” or “No, a non-rectangular number”.

Self-Correction of Infeasible Solutions

The teacher asked the children in Crocodile group if it is possible to park thefive cars in two rows and make a rectangle. This time, they were made to try it out on two different ferries with two and three parking columns, respectively. Zahra, Gertrude, and Esmeralda started parking on one ferry as Marcus, Noel, and Douglas started parking on the other ferry. The boys worked in the following way:

Marcus and Douglas parked the cars in a two by two rectangle, and Marcus put thefifth car in a different direction, as inFigure 5, since the size of the cars allowed this to be a nice rectangle. Noel got involved and removed thefifth car. While pointing [at] and explaining about the four edges, Noel reassured [Douglas and Marcus] that there was no need for afifth car as the four cars were making solid edges of the rectangle. Afterwards, Marcus took over and put back thefifth car that was removed by Noel and added a sixth car, and explained that it would otherwise be impossible to make a rectangle. During this part of the activity, the tea-cher did not comment on or interfere with the children’s activity. The children did this self-correcting activity all on their own initiative.

In summary, Marcus tried the mathematically inventive, but practically infeasible, solution of park-ing one car perpendicular to the other cars, as inFigure 5. Moreover, Noel and Marcus demon-strated to their peers how they could make a rectangle by removing or adding one car.

Taking Teacher-Independent Mathematical Initiatives

When the children in the Caymans group found out that parkingfive cars in a rectangular shape on a road ferry with two parking columns does not work, the teacher replaced the ferry with two park-ing columns with the ferry with three parkpark-ing columns. The Caymans children, together, found that parking the cars in a rectangular shape on the ferry with three parking columns still did not work. When the teacher asked where to put theflash card marked with number five, Oliver responded “the red one”, meaning the paper with a red cross and the text “no, a non-rectangular number”.

After this, the teacher gave out a sixth car. Without teacher-interference, Wilma and Victor worked together and parked the car so that the cars together formed a rectangular pattern. Sub-sequently, they took theflash card marked with number six and put it on the paper, saying “Yes, a rectangular number.”

Figure 4.Adam concluded that three cars does not make a rectangular shape.

Next, the teacher gave out a seventh car. Wilma moved the seventh car between two different parking columns, followed by Victor who did the same and concluded with a“No”. The teacher then changed the ferry to a ferry with two parking columns and said,“Should we try this instead?” The children parked the cars on the ferry with two columns and found that they could not make a rectangle. The teacher then changed the ferry to a ferry withfive parking columns and said, “Should we try this instead?” The children cooperated in arranging the cars with three cars in front of four cars. Adam counted the seven cars by pointing at them, took theflash card marked with number seven and put it on the paper marked“No, a non-rectangular number” without the teacher asking for it.

The three consecutive cases withfive, six, and seven cars show that the children in the Caymans group had started to work independently of the teacher by making decisions and taking the initiat-ive themselves according to the rules of the game, except for changing ferries. Without the teacher’s prompting, the childrenfirst cooperatively tried different ways of arranging the cars, then picked a flash card marked with a number, and finally sorted the flash card as a rectangular number or a non-rectangular number. This kind of independent initiative was not observed among the Alligators. The interaction between Alligator children and teacher followed this pattern. First, the teacher gave one ferry at a time and invited the children to arrange the cars. Next, the teacher asked them to identify whether or not the cars form a rectangular shape. Finally, the teacher prompted them tofind the numbered flash card and to sort it as a rectangular or non-rectangular number. Another feature in the Alligators group was that the children did separate parts of the tasks. For example, Harold and Youssef managed arranging the cars while Monique, who joined the activity later, looked up theflash card in question and put it on the appropriate paper marked, “Yes, a rec-tangular number” or “No, a non-rectangular number”.

A Difficult Case: Number Nine

The Caymans group put eight cars in a four by two pattern on the ferry withfive parking columns and got a ninth car. The children tried, but did not manage, to make a rectangle of nine cars in four columns (on the ferry withfive columns) and were about to sort the number as non-rectangular when the teacher intervened and gave them the ferry with two columns. The children concluded that arranging nine cars on the ferry with two parking columns also did not work. The teacher inter-vened again by giving them the ferry with three parking columns, with the following results:

Wilma and Adam movedfive cars to the new ferry in one column. Victor said, “I don’t think,” as Wilma and Adam went on placing the remaining four cars in the second parking column. The teacher interfered“Why don’t you use all the three rows?” and pointed at the three parking columns. The teacher repeated, “Try to use all the three rows”. While Victor was still holding the number nine card, Wilma and Adam went on parking the cars. Wilma said,“I don’t think so,” and so said Adam as well. They parked two cars in one column, three cars in the middle and four cars in the third parking column. When they were done, Victor interfered, moved one car from the column with four cars to the column with two cars, and thus arranged a three by three pat-tern.“Yes!” exclaimed Wilma, relieved, and she and Adam clapped hands excitedly. Adam counted the cars by pointing, but missed one and got only to eight and started to look for theflash card marked with number eight. Victor started to count and counted to nine cars and then put theflash card marked with number nine on the paper marked,“Yes, a rectangular number”. Adam looked at the paper with the four flash cards numbered with four, six, eight and nine and excitedly exclaimed,“Yes, now there are four” (meaning the four flash cards among the rectangular numbers).

This excerpt shows that the teacher in this case needed to interfere in the Caymans group by chan-ging ferry. Also the children took turns in observing and working. For example, Victor was observ-ing while Wilma and Adam tried an arrangement. As Wilma and Adam stopped workobserv-ing and as they hypothesized“I don’t think so”, Victor took over the working initiative and found a rectangu-lar arrangement of the nine cars. Wilma and Adam expressed their joy when Victor provided the final solution and so did Adam when he found that there were four numbers sorted as rectangular numbers. The Cayman children seemed to have developed emotional sympathy for the rectangular

numbers. The cooperative work and the emotions shown were similar to those demonstrated when the Caymans worked with 10 cars:

When Adam and Wilma hadfirst parked them sparsely and thus could not make a rectangular pattern, Wilma said, “No!” with a falling pitch as if disappointed. Then after a few seconds Wilma leaned forward and exclaimed,“Wait, wait!” and started to pack the cars more densely together with Adam and managed to fit the ten cars in a rectangular shape. As Adam sorted number ten as a rectangular number he said,“There!” and waved his arms.

Discussion

The present study asked what kinds of engagement and mathematical activities the children were involved in as they played a game on parking different given numbers of identically-sized Lego cars in a rectangular pattern. It was evident from the data that the children engaged with the task both emotionally and cognitively. Their excitement, joy, and disappointment were evident. The children seemed to engage in the activity as though it was a realistic task; for example, some children had personal real-life experience of such road ferries. In addition, the other children could see and count the number of parking columns on the pictures of real ferries and some children made the humming sound of a car, which could possibly imply that they viewed the game as play. With respect to the mathematical content of the game and the teacher’s interventions, the children’s play was guided (Cutter-Mackenzie et al., 2014; Edwards & Cutter-Mackenzie, 2011). Another aspect of the guided play was the children’s teamwork, which is in contrast to several studies con-ducted with individuals, the typical approach to research on learning outcomes (e.g., Battista et al.,

1998; Bertelli et al.,1998; English,1991; Fisher et al.,2013; Fox,2005; Habgood & Ainsworth,2011; Shiakalli,2014). The children in Alligators (the youngest group) worked as a team; as one child arranged the pattern of the cars, another child counted and identified the number of cars, and a third child identified the number symbol and where to put the flash card. This cooperative play in teams occurred in Crocodiles also, when the boys and the girls worked for a while in two separate groups as they tried to make a rectangular shape offive cars and rejected the suggestion of parking the cars as shown inFigure 5. In summary, the realistic context of the guided play activity seemed to facilitate a natural and emotionally rich environment, an immersiveflow activity, in the sense that the children worked together, made playful sounds, and expressed feelings about their mathemat-ical discoveries and achievements. We interpret thisfinding as demonstrating that the children per-ceived the game as (guided) play. A methodological reflection is that these results do not allow the classification of this designed play as what Habgood and Ainsworth (2011) termed an“intrinsic game”, in that it integrates the learning into the game. Such a classification would require continu-ously evaluating the learning outcome during the game. However, if we alter their definition of intrinsic game from integrating learning outcomes into the game to integrating learning opportu-nities into the game, we can classify the designed activity as an“intrinsic game with respect to learn-ing opportunities”. Accordingly, a coherent alternate definition of an “extrinsic game with respect to learning opportunities” would be that it rewards the learner with separate play not (explicitly) providing learning opportunities for the same learning object. These alternate definitions would be easier to operationalize than the original definition offered by Ainsworth and Habgood.

There were several opportunities for cognitive engagement during the play. The children in all three groups counted orally and identified number symbols (cf. Charlesworth,2005). During play, the children together constructed and named rectangular shapes by parking the cars and used, for example, the number of corners as an argument for a shape being rectangular, hence making declarative statements about the rectangular shape (Clements et al.,1999). In detail, they made sup-positions about whether or not a number was rectangular and in both actions and words provided arguments for their suppositions thus expressing themselves in multiple ways while reasoning and negotiating. Such declarative statements were similar to those identified in Clements et al. (1999). Even the Alligators, the youngest children, seemed tofind constructing and classifying a shape as

rectangular easy, as did Harold and Youssef, shown inFigure 3, which is in line with thefindings of Clements et al. (1999), Elia and Gagatsis (2003), and Shiakalli (2014). For the case of two parking columns, all groups of children worked systematically tofind rectangular numbers, as shown in

Figure 4. Even the four-year-old Alligator children showed the beginnings of systematic examin-ation of the task as they forecasted,“We need one more [car]” in order to complete a rectangular shape, demonstrating that they were aware of both the rectangular shape and the task they were attempting. In the case of three orfive parking columns, all groups of children explored the parking possibilities in a less systematic but still purposeful way. The Crocodiles children (the oldest group) were able, independently of the teacher, to discern between feasible and infeasible solutions and to provide arguments for their conclusions. These results are similar to those of English (1991) in the sense that young children both used systematic exploration and expressed trial-and-error strategies. In summary, it was evident that this game, arranged as guided play, used several mathematical con-cepts, for example quantity, number symbols, shapes, mathematical communication, and argumen-tation. Steinbring (1997) emphasizes using a multimodal approach to create mathematical meaning for students and it seems that this enacted game constituted guided play on rectangular numbers and also provided a meaningful learning environment for preschool children. In fact, while playing, the children developed a schema for the mathematical activities in this game as they soon managed to work partly independently of the teacher (Van Oers,2010) in that they could construct rectangu-lar numbers and distinguish them from non-rectangurectangu-lar numbers. This could possibly mean that figurate numbers are suitable for preschool mathematics and not only school mathematics. The authors believe that this game is an activity that paves the way for concept development in geometry (e.g., Suzuki,2009) and number sense development in primary school because these are connected tofigurate numbers such as multiplication and division, as also pointed out by Barmby et al. (2009) and Bolden et al. (2013).

In guided play, the teacher fulfils an important role in monitoring the children’s work (Björklund et al.,2020), as was demonstrated in the teacher’s recurrent interventions. Among the young Alli-gators, the teacher often prompted the children by giving out cars, changing the ferry when required, and asking if theflash card marked with the number should be put among the rectangular or non-rectangular numbers. The Caymans and Crocodiles were able to quickly learn the game and proactively acted on their own initiative in adding new cars and deciding whether or not a number was rectangular; however, the teacher still prompted them by changing the ferry when appropriate. In the Caymans and Crocodiles, the teacher acted as a supporter and facilitator of the children’s mathematical activities (Pramling Samuelsson & Asplund Carlsson,2008). It is common practice among pre-primary teachers to observe the mathematical content in a conversation and provide prompts with new material and ideas when needed, the approach also used here (Björklund,

2015). This study also demonstrated how preschool teachers can intentionally plan and adapt chil-dren’s play into a mathematical learning moment through guided play based in a realistic context. As indicated in thefindings, this pedagogical play engaged the children in multiple mathematical activities, which is in line with the idea of play and learning being inseparable entities in preschool (Pramling Samuelsson & Asplund Carlsson,2008; Pramling Samuelsson & Johansson, 2006). By exploring the properties of numbers through concrete manipulation of objects in their world whilst discussing and modifying their responses in interaction with one another, children experience both hypothesis formation and proof. This should create opportunities to learn mathematics through play. This guided play is equivalent tofinding out if a number is prime since all non-prime numbers can be expressed as rectangular numbers, where the two edges constitute one factorization of the rectangular number. Hence, this guided play is a concrete way in which to manipulate and visualize prime numbers and composite numbers through a game inspired byfigurate numbers. Since this study did not explore the learning outcome of the designed play only the engagement and activities that it created, the authors suggest, for future research, exploring the children’s long-term learning outcomes from this game. Another suggestion for future research is to design other activities inspired byfigurate numbers and try them out as guided play activities in preschool and primary

school or activities in school leisure time. Finally, the authors would like to bring this approach of figurate numbers to the attention of preschool teachers and preschool teacher educators, so that they can try it out as a possible approach to purposefully embed mathematics within the children’s world of play.

Disclosure Statement

No potential conflict of interest was reported by the author(s).

ORCID

Jöran Petersson http://orcid.org/0000-0001-5609-0752

Kassahun Weldemariaam http://orcid.org/0000-0002-7017-0246

References

Andrews, P., & Sayers, J. (2015). Identifying opportunities for grade one children to acquire foundational number sense: Developing a framework for cross cultural classroom analyses. Early Childhood Education Journal, 43(4), 257–267.https://doi.org/10.1007/s10643-014-0653-6

Antell, S. E., & Keating, D. P. (1983). Perception of numerical invariance in neonates. Child Development, 54(3), 695– 701.https://doi.org/10.2307/1130057

Barmby, P., Harries, T., Higgins, S., & Suggate, J. (2009). The array representation and primary children’s under-standing and reasoning in multiplication. Educational Studies in Mathematics, 70(3), 217–241.https://doi.org/ 10.1007/s10649-008-9145-1

Battista, M. T., Clements, D. H., Arnoff, J., Battista, K., & Borrow, C. V. A. (1998). Students’ spatial structuring of 2D arrays of squares. Journal for Research in Mathematics Education, 29(5), 503–532.https://doi.org/10.2307/749731

Bertelli, R., Joanni, E., & Martlew, M. (1998). Relationship between children’s counting ability and their ability to reason about number. European Journal of Psychology of Education, 13(3), 371–383. https://doi.org/10.1007/ BF03172951

Björklund, C. (2015). Pre-primary school teachers’ approaches to mathematics education in Finland. Journal of Early Childhood Education Research, 4(2), 69–92.

Björklund, C., Magnusson, M., & Palmér, H. (2018). Teachers’ involvement in children’s mathematizing – Beyond dichotomization between play and teaching. European Early Childhood Education Research Journal, 26(4), 469– 480.https://doi.org/10.1080/1350293X.2018.1487162

Björklund, C., van den Heuvel-Panhuizen, M., & Kullberg, A. (2020). Research on early childhood mathematics teaching and learning. ZDM Mathematics Education, 52(4), 607–619. https://doi.org/10.1007/s11858-020-01177-3

Bolden, D., Barmby, P., & Harries, T. (2013). A representational approach to developing primary ITT students’ confi-dence in their mathematics. International Journal of Mathematical Education in Science and Technology, 44(1), 70– 83.https://doi.org/10.1080/0020739X.2012.690899

Booth, J., & Siegler, R. (2008). Numerical magnitude representations influence arithmetic learning. Child Development, 79(4), 1016–1031.https://doi.org/10.1111/j.1467-8624.2008.01173.x

Charlesworth, R. (2005). Prekindergarten mathematics: Connecting with national standards. Early Childhood Education Journal, 32(4), 229–236.https://doi.org/10.1007/s10643-004-1423-7

Charlesworth, R., & Leali, S. A. (2012). Using problem solving to assess young children’s mathematics knowledge. Early Childhood Education Journal, 39(6), 373–382.https://doi.org/10.1007/s10643-011-0480-y

Clements, D. H., & Sarama, J. (2007). Early childhood mathematics learning. In J. Frank & K. Lester (Eds.), Second handbook of research on mathematics teaching and learning: A project of the national council of teachers of math-ematics (Vol. 1, pp. 461–555). Information Age Pub.

Clements, D. H., & Sarama, J. (2011). Early childhood teacher education: The case of geometry. Journal of Mathematics Teacher Education, 14(2), 133–148.https://doi.org/10.1007/s10857-011-9173-0

Clements, D. H., Swaminathan, S., Hannibal, M. A. Z., & Sarama, J. (1999). Young children’s concepts of shape. Journal for Research in Mathematics Education, 30(2), 192–212.https://doi.org/10.2307/749610

Cross, D. I., Adefope, O., Lee, M. Y., & Perez, A. (2012). Hungry for early spatial and algebraic reasoning. Teaching Children Mathematics, 19(1), 42–49.https://doi.org/10.5951/teacchilmath.19.1.0042

Cutter-Mackenzie, A., Edwards, S., Moore, D., & Boyd, W. (2014). Young children’s play and environmental education in early childhood education. Springer International Publishing.

Doverborg, E., & Pramling-Samuelsson, I. (2000). To develop young children’s conception of numbers. Early Child Development and Care, 162(1), 81–107.https://doi.org/10.1080/0300443001620107

Duval, R. (2006). A cognitive analysis of problems of comprehension in a learning of mathematics. Educational Studies in Mathematics, 61(1–2), 103–131.https://doi.org/10.1007/s10649-006-0400-z

Edwards, S., & Cutter-Mackenzie, A. (2011). Environmentalising early childhood education curriculum through ped-agogies of play. Australasian Journal of Early Childhood, 36(1), 51–59. https://doi.org/10.1177/ 183693911103600109

Ekdahl, A.-L. (2020). Different learning possibilities from the same activity—Swedish preschool teachers’ enactment of a number relation activity. Scandinavian Journal of Educational Research, 1–14. https://doi.org/10.1080/ 00313831.2020.1739131

Elia, I., & Gagatsis, A. (2003). Young children’s understanding of geometric shapes: The role of geometric models. European Early Childhood Education Research Journal, 11(2), 43–61.https://doi.org/10.1080/13502930385209161

English, L. D. (1991). Young children’s combinatoric strategies. Educational Studies in Mathematics, 22(5), 451–474.

https://doi.org/10.1007/BF00367908

Fisher, K. R., Hirsh-Pasek, K., Newcombe, N., & Golinkoff, R. (2013). Taking shape: Supporting preschoolers’ acqui-sition of geometric knowledge through guided play. Child Development, 84(6), 1872–1878.https://doi.org/10. 1111/cdev.12091

Fox, J. (2005). Child-initiated mathematical patterning in the pre-compulsory years. In H. L. E. A. Chick (Ed.), Proceedings of the 29th annual conference of the international group for the psychology of mathematics education, PME 29, Melbourne, Australia, July 10–15, 2005 (Vol. 1–4, pp. 313–320). University of Melbourne, Department of Science and Mathematics Education.

Gardner, M. (2001). The colossal book of mathematics: Classic puzzles, paradoxes, and problems: Number theory, alge-bra, geometry, probability, topology, game theory, infinity, and other topics of recreational mathematics. Norton. Habgood, M. P. J., & Ainsworth, S. E. (2011). Motivating children to learn effectively: Exploring the value of intrinsic

integration in educational games. Journal of the Learning Sciences, 20(2), 169–206. https://doi.org/10.1080/ 10508406.2010.508029

Häikkilä, M., & Sahlström, F. (2003). Om användning av videoinspelning i fältarbete [On using video recording in field work]. Pedagogisk Forskning i Sverige, 8(1/2), 24–41.

Hannula, M. S. (2002). Attitude towards mathematics: Emotions, expectations and values. Educational Studies in Mathematics, 49(1), 25–46.https://doi.org/10.1023/A:1016048823497

Hannula, M. S. (2012). Exploring new dimensions of mathematics-related affect: Embodied and social theories. Research in Mathematics Education, 14(2), 137–161.https://doi.org/10.1080/14794802.2012.694281

Hermerén, G. (2011). Good research practice. The Swedish Research Council. Katz, V. J. (1998). A history of mathematics: An introduction (2nd ed.). Longman.

Kilday, C. R., & Kinzie, M. B. (2009). An analysis of instruments that measure the quality of mathematics teaching in early childhood. Early Childhood Education Journal, 36(4), 365–372.https://doi.org/10.1007/s10643-008-0286-8

Larsson, K., Pettersson, K., & Andrews, P. (2017). Students’ conceptualisations of multiplication as repeated addition

or equal groups in relation to multi-digit and decimal numbers. The Journal of Mathematical Behavior, 48, 1–13.

https://doi.org/10.1016/j.jmathb.2017.07.003

Norris, S. (2002). The implication of visual research for discourse analysis: Transcription beyond language. Visual Communication, 1(1), 97–121.https://doi.org/10.1177/147035720200100108

Papic, M. (2007). Promoting repeating patterns with young children– More than just alternating colours! Australian Primary Mathematics Classroom, 12(3), 8–13.

Papic, M. M., Mulligan, J. T., & Mitchelmore, M. C. (2011). Assessing the development of preschoolers’ mathematical patterning. Journal for Research in Mathematics Education, 42(3), 237–268. https://doi.org/10.5951/ jresematheduc.42.3.0237

Pramling Samuelsson, I., & Asplund Carlsson, M. (2008). The playing learning child: Towards a pedagogy of early childhood. Scandinavian Journal of Educational Research, 52(6), 623–641. https://doi.org/10.1080/ 00313830802497265

Pramling Samuelsson, I., & Johansson, E. (2006). Play and learning—Inseparable dimensions in preschool practice. Early Child Development and Care, 176(1), 47–65.https://doi.org/10.1080/0300443042000302654

Ramani, G. B., & Siegler, R. S. (2008). Promoting broad and stable improvements in low-income children’s numerical knowledge through playing number board games. Child Development, 79(2), 375–394.https://doi.org/10.1111/j. 1467-8624.2007.01131.x

Reikerås, E. (2020). Relations between play skills and mathematical skills in toddlers. ZDM Mathematics Education, 52(4), 703–716.https://doi.org/10.1007/s11858-020-01141-1

Saracho, O. N., & Spodek, B. (2009). Educating the young mathematician: The twentieth century and beyond. Early Childhood Education Journal, 36(4), 305–312.https://doi.org/10.1007/s10643-008-0293-9

Shiakalli, M. A. (2014). Constructing squares as a mathematical problem solving process in pre-school. Review of Science, Mathematics and ICT Education, 8(1), 43–64.https://doi.org/10.26220/rev.2039

Steinbring, H. (1997). Epistemological investigation of classroom interaction in elementary mathematics teaching. Educational Studies in Mathematics, 32(1), 49–92.https://doi.org/10.1023/A:1002919830949

Stephen, C. (2010). Pedagogy: The silent partner in early years learning. Early Years: An International Research Journal, 30(1), 15–28.https://doi.org/10.1080/09575140903402881

Suzuki, J. (2009). Modern geometric algebra: A (very incomplete!) survey. The Mathematics Teacher, 103(1), 26–33.

https://doi.org/10.5951/MT.103.1.0026

Synodi, E. (2010). Play in the kindergarten: The case of Norway, Sweden, New Zealand and Japan. International Journal of Early Years Education, 18(3), 185–200.https://doi.org/10.1080/09669760.2010.521299

Van de Rijt, B., Van Luit, J., & Pennings, A. (1999). The construction of the Utrecht early mathematical competence scales. Educational and Psychological Measurement, 59(2), 289–309.https://doi.org/10.1177/0013164499592006

Van Oers, B. (2010). Emergent mathematical thinking in the context of play. Educational Studies in Mathematics, 74 (1), 23–37.https://doi.org/10.1007/s10649-009-9225-x

Vogel, R. (2005). Patterns—A fundamental idea of mathematical thinking and learning. Zentralblatt für Didaktik der Mathematik, 37(5), 445–449.https://doi.org/10.1007/s11858-005-0035-z

Warfield, J. (2001). Teaching kindergarten children to solve word problems. Early Childhood Education Journal, 28 (3), 161–167.https://doi.org/10.1023/A:1026591117867

Wynn, K. (1992). Addition and subtraction by human infants. Nature, 358(6389), 749–750.https://doi.org/10.1038/ 358749a0