Mathematical Analysis of Forced Convective Flow Due to Stretching Sheet and Instabilities of Natural Convective Flow

(1)

Mälardalen University Press Dissertations No. 226

MATHEMATICAL ANALYSIS OF FORCED CONVECTIVE

FLOW DUE TO STRETCHING SHEET AND

INSTABILITIES OF NATURAL CONVECTIVE FLOW

Prashant G Metri 2017

(2)

ISSN 1651-4238

(3)

Mälardalen University Press Dissertations No. 226

MATHEMATICAL ANALYSIS OF FORCED CONVECTIVE FLOW DUE TO STRETCHING SHEET AND INSTABILITIES OF NATURAL CONVECTIVE FLOW

Prashant G Metri

Akademisk avhandling

som för avläggande av filosofie doktorsexamen i matematik/tillämpad matematik vid Akademin för utbildning, kultur och kommunikation kommer att offentligen försvaras måndagen den 29 maj 2017, 13.15 i Kappa, Mälardalens högskola, Västerås.

Fakultetsopponent: Adjunct Professor Rebei Bel Fdhila, Mälardalens högskola

(4)

Abstract

The investigations presented in the thesis are theoretical studies of magnetohydrodynamic flows, heat and mass transfer in Newtonian/non-Newtonian cooling liquids, due to horizontal/vertical stretching sheet. The theoretical studies include the effect of magnetic field, uniform and non-uniform heat source/ sink (flow and temperature dependent heat source/sink) effects. The considered problems include flow of viscous fluids in the presence of applied magnetic field and electric field with first order chemical reactions. The viscous incompressible Newtonian fluid flow in porous medium with Darcy-Forchheimmer model, electrically conducting fluid and nanofluid is studied. We introduce innovative techniques for finding solutions of highly nonlinear coupled boundary value problems such as Runge-Kutta method, Perturbation method and Differential Transform Method (DTM).

Chapter 1-2 gives a brief introduction. Chapter 3 focuses on Lie group analysis of MHD flow and heat transfer over a stretching sheet. The effects of viscous dissipation, uniform heat source/sink and MHD on heat transfer are addressed. In Chapter 4-6 we examined the laminar flow, thermocapillary flow of a nanoliquid thin film over an unsteady stretching sheet in presence of MHD and thermal Radiation in different situations. An effective medium theory (EMT) based model is used for the thermal conductivity of the nanoliquid. Metal and metal oxide nanoparticles are considered in carboxymethyl cellulose (CMC) - water base liquid. In Chapter 7-9 we analyzed, heat and mass transfer in MHD, mixed convection, viscoelastic fluid flow, non-Darcian flow due to stretching sheet in presence of viscous dissipation, non-uniform heat source/sink and porous media have been investigated in different situations. MHD and viscous dissipation have a significant influence on controlling of the dynamics. In Chapter 10 the linear stability of Maxwell fluid-nanofluid flow in a saturated porous layer is examined theoretically when the walls of the porous layers are subjected to time-periodic temperature modulations. A modified Darcy-Maxwell model is used to describe the fluid motion, and the nanofluid model used includes the effects of the Brownian motion. The thermal conductivity and viscosity are considered to be dependent on the nanoparticle volume fraction.

In Chapter 11 we studied MHD flow in a vertical double passage channel taking into account the presence of the first order chemical reactions. The governing equations are solved by using a regular perturbation technique valid for small values of the Brinkman number and a DTM valid for all values of the Brinkman number.

ISBN 978-91-7485-323-0 ISSN 1651-4238

(5)

Once you start working on something, don’t be afraid of failure and don’t abandon it. People who work sincerely are the happiest.

(6)

(7)

I dedicate this thesis to my beloved PARENTS Smt. Sanjivani Metri

and

(8)

(9)

Acknowledgements

This dissertation is the end of my journey in obtaining my doctoral degree. This dissertation has been kept on track and been seen through to completion with the support and encouragement of numerous people including my well wishers, my friends, colleagues and various institutions. At the end of my dissertation I would like to thank all those people who made this dissertation possible and an unforgettable experience for me. At the end of my disserta-tion, it is a pleasant task to express my thanks to all those who contributed in many ways to the success of this study and made it an unforgettable experience for me.

Looking back at my years working in the Division of Applied Mathemat-ics, UKK, M¨alardalen University, I feel blessed at every step along the way. It has been such a wonderful journey, not just because of great work carried under the roof of the department, but many wonderful people that I got to know and become friends with.

I start with thanking my research supervisor, Professor Sergei Silvestrov, you have created the invaluable space for me to do this research and develop myself as a researcher in the best possible way. His concept of with freedom comes responsibility has made me understand several aspects of research.

I wish to express my sincere gratitude to Dr. Milica Ranˇci´c for your help and sincere interest in all technical and conceptual questions I have had.

I am also very grateful to Professor Bhimaraya Metri, Director, IIM Tiruchirappalli, India who were always so helpful and provided me with their assistance throughout my studies.

I owe everything to Professor Subhas Abel, Department of Mathematics, Gulbarga University, India who gave me the required thrust to enter into my research career. The interactions, on the related topics, with him are the best ones I had in my career. His keen interest on me and the constant motivation has kept me going in my journey.

(10)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow

A very special thanks to Professor J. C. Umavathi, Department of Math-ematics, Gulbarga University, India for her invaluable advice and feedback on my research and for always being so supportive of my work.

I am also extremely indebted to Dr. Mahesha. Narayana, M. S. Ramaiah university of Applied Sciences, Bangalore, India for making me learn the computational techniques at the appropriate time in my endeavor of solving research problems included in this thesis.

I also take opportunity to thank all my collaborators, Professor K. Va-jravelu, Department of Mathematics, Mechanical, Material and Aerospace Engineering, University of Central Florida, Orlando, FL 32816, USA, Pro-fessor J. Pratapkumar, Department of Mathematics, Gulbarga University, India and Emanuel Guariglia, Department of Mathematics, University of Salerno, Italy.

I would like to thank Karl Lundeng˚ard, who as a good friend, is always willing to help and give his best suggestions.

I would like to thank all the collegues of Division of Applied Mathematics, UKK, M¨alardalen University for their constant support during my stay.

Last but not least, I would like to pay high regards to my family for their sincere encouragement and inspiration throughout my research work and lifting me uphill this phase of life. I owe everything to them. Besides this, several people have knowingly and unknowingly helped me in the successful completion of this doctoral study. I heartily thankful to one and all for their constant support.

V¨aster˚as, March, 2017 Prashant G Metri

(11)

List of Papers

This thesis contains the following papers:

Paper A. Metri, Prashant G. Guariglia, Emanuel. Silvestrov, Sergei (2017), Lie Group Analysis for MHD Boundary Layer Flow and Heat Transfer over a Stretching Sheet in presence of Viscous Dissipation and Uniform Heat Source/Sink, International conference in nonlinear problems in aviation and aerospace (ICNPAA), La Rochelle, France, AIP conf. Proc. 1798. 020096; doi:10.1063/1.4972688.

Paper B. Metri, Prashant G. Narayana, Mahesha. Silvestrov, Sergei (2017), Hy-pergeometric Steady Solution of Hydromagnetic Nano Liquid Film Flow over an Unsteady Stretching Sheet, International conference in nonlinear problems in aviation and aerospace (ICNPAA), La Rochelle, France, AIP conf. Proc. 1798. 020097; doi:10.1063/1.4972689.

Paper C. Narayana, Mahesha. Metri, Prashant G. Silvestrov, Sergei (2017), Ther-mocapillary Flow of a non-Newtonian Nanoliquid Film over an Unsteady Stretching Sheet, International conference in nonlinear problems in aviation and aerospace (ICNPAA), La Rochelle, France, AIP conf. Proc. 1798. 020109; doi:10.1063/1.4972701.

Paper D. Metri, Prashant G. Abel, Subhas. Tawade, Jagdish. Metri, Pushpanjali G. (2016), Fluid Flow and Radiative Nonlinear Heat Transfer in a Liquid Film over an Unsteady Stretching Sheet, 7th International conference on mechanical and aerospace engineering (ICMAE), London, United Kingdom, pp.83-87, doi:10.1109/ICMAE.2016.7549513.

Paper E. Metri, Prashant G. Metri, Pushpanjali G. Abel, Subhas. Silvestrov, Sergei (2016), Heat Transfer in MHD Mixed Convection Viscoelastic Fluid Flow over a Stretching Sheet Embedded in a Porous Medium with Viscous Dissipation and non-Uniform Heat Source/Sink, IX International Confer-ence on Computational Heat and Mass Transfer (ICCHMT), Procedia En-gineering 157, 309–316.

(12)

Paper F. Metri, Prashant G. Bablad, Veena. Metri, Pushpanjali G. Abel, Sub-has. Silvestrov, Sergei (2016), Mixed Convection Heat Transfer in MHD Non–Darcian Flow Due to an Exponential Stretching Sheet Embedded in a Porous Medium in Presence of Non-uniform Heat Source/Sink, in Silvestrov S., Rancic M.,(eds.) Engineering Mathematics I: Springer Proceedings in Mathematics & Statistics 178, 187–201.

Paper G. Metri, Prashant G. Abel, Subhas. Silvestrov, Sergei (2016), Heat and Mass Transfer in MHD Boundary Layer Flow over a Nonlinear Stretch-ing Sheet in a Nanofluid with Convective Boundary Conditions and Viscous Dissipation, in Silvestrov S., Rancic M.,(eds.) Engineering Mathematics I: Springer Proceedings in Mathematics & Statistics 178, 203–219.

Paper H. Jawali, Umavathi. Vajravelu, Kuppalapalle. Metri, Prashant G. Silve-strov, Sergei (2016), Effect of Time-Periodic Boundary Temperature Modu-lations on the Onset of Convection in a Maxwell Fluid-Nanofluid Saturated Porous Layer, in Silvestrov S., Rancic M.,(eds.) Engineering Mathematics I: Springer Proceedings in Mathematics & Statistics 178, 221–245.

Paper I. Jada, Pratap Kumar. Jawali, Umavathi. Metri, Prashant G. Silvestrov, Sergei (2016), Effect of First Order Chemical Reaction on Magneto Convec-tion in a Verticle Double Passage Channel, in Silvestrov S., Rancic M.,(eds.) Engineering Mathematics I: Springer Proceedings in Mathematics & Statis-tics 178, 247–279.

(13)

Parts of the thesis have been presented at the following international conferences:

1. 9th International Conference on Computational Heat and Mass Trans-fer - ICCHMT 2016, Cracow, Poland, May 23-26, 2016.

2. International conference in nonlinear problems in aviation and aerospace - ICNPAA 2016, La Rochelle, France, July 5-8, 2016.

3. 7th International conference on mechanical and aerospace engineering - ICMAE 2016, London, United Kingdom, July 18-22, 2016.

(14)

(15)

Preface

The investigations presented in the thesis are theoretical studies of magne-tohydrodynamic flows, heat and mass transfer in Newtonian/non-Newtonian cooling liquids, due to horizontal/vertical stretching sheet. The theoretical studies include the effect of magnetic field, uniform and non-uniform heat source/sink (flow and temperature dependent heat source/sink) effects.

The problems considered flow of a viscous fluids in the presence of applied magnetic field and electric field with first order chemical reactions. The viscous incompressible Newtonian fluid flow in porous medium with Darcy-Forchheimmer model, electrically conducting fluid and nanofluid is studied.

We introduced innovative techniques for finding solutions of highly nonlin-ear coupled boundary value problems, such as Runge-Kutta method, Pertur-bation method and Differential Transform Method (DTM). These technique aims to combine the strength of both analytical and numerical methods to produce efficient hybrid algorithm. The problems in the non-linear regime of free or forced or mixed convection involving any liquid are quite formidable to solve analytically or numerically. The thesis throws light on many of such challenging problems. The thesis is organized into eleven chapters.

Chapter 1 is introductory nature and presents the objective and scope of the thesis. A detailed literature survey of stretching sheet problem relevant to the thesis is also presented in the chapter.

Chapter 2 gives a brief introduction about various non-Newtonian liq-uids, their properties and applications. The chapter also concerns with basic equations of conservation of mass, linear momentum and energy of Newtonian/non-Newtonian liquids, approximations used and dimensionless parameters involved in the problems investigated in the thesis.

Chapter 3 focuses on the Lie group analysis of boundary layer flow and heat transfer over a stretching sheet. The effects of viscous dissipation, uniform heat source/sink and magnetohydrodynamics on heat transfer is

(16)

ad-Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow dressed. The governing partial differential equations are reduced to a system of ordinary differential equations by the scaling symmetries. The symmetry groups admitted by the corresponding boundary value problem are obtained by using special Lie group transformations. The scaling of group transfor-mations is applied to the governing equations. The system remains invariant due to some relation among the parameters of the transformations. The equations along with boundary conditions are solved numerically.

In Chapter 4 an analysis is made to study the laminar flow and heat transfer characteristics of nanoliquid film over an unsteady stretching sheet. The highly nonlinear partial differential equations governing flow and heat transport are simplified using similarity transformation. The analytical solu-tions of the resulting ordinary differential equasolu-tions are obtained for a special case of nanoliquid film using hypergeometric power series functions, and from which the analytical solutions of the original problem are presented. Nusselt number and skin friction coefficient is discussed analytically.

In Chapter 5 we examine the influence of surface tension on the laminar flow of a thin film of a non-Newtonian nanoliquid over an unsteady stretching sheet is considered. Surface tension is assumed vary linearly with tempera-ture. An effective medium theory (EMT) based model is used for the thermal conductivity of the nanoliquid. Metal and metal oxide nanoparticles are con-sidered in carboxymethyl cellulose (CMC)- water base liquid. The unsteady boundary layer equations are transformed to a system of non-linear ordi-nary differential equations with the application of similarity transformations. Resultant two-point boundary value problem is solved numerically using a shooting method together with Runge-Kutta-Fehlberg and Newton-Raphson schemes. The effect of surface tension on the dynamics of the considered problem is presented graphically and analyzed in detail.

Chapter 6 concern with a mathematical analysis of MHD flow and heat transfer of laminar liquid film flow over an unsteady stretching sheet in pres-ence of thermal radiation. The effect of thermal radiation using nonlinear Rosseland approximations is investigated. The flow of a thin fluid film and subsequent heat transfer from the stretching surface is investigated with the aid of similarity transformation. The transformation enables to reduce the unsteady boundary layer equations to a system of non-linear ordinary differ-ential equations. Numerical solution of resulting nonlinear differdiffer-ential equa-tions is found by using efficient shooting technique. Present analysis shows that the combined effect of magnetic field and thermal radiation is to enhance the thermal boundary layer thickness.

(17)

In Chapter 7 a numerical model is developed to study MHD mixed con-vection viscoelastic fluid flow over a stretching sheet embedded in a porous medium in presence of viscous dissipation, and non-uniform heat source/sink have been investigated. The variation of porosity is assumed. Effect of vis-cous dissipation is also included in the study. Here two types of different heating processes are considered namely, PST (prescribed surface temper-ature) and PHF (prescribed heat flux). Similarity transformation is used to convert the governing partial differential equations into a set of coupled, non-linear ordinary differential equations. The shooting method is used to obtain the numerical solutions of the resulting boundary value problems. Some of important findings reported in this work reveal that the effect of viscous dissipation and non-uniform heat source/sink and significant impact in controlling the rate of heat transfer in the boundary layer region.

In Chapter 8 a mathematical analysis is carried out to describe mixed convection heat transfer in magnetohydrodynamic non-Darcian flow due to an exponential stretching sheet embedded in a porous medium in the pres-ence of a non-uniform heat source/sink. Approximate analytical similarity solutions of the highly non-linear momentum and energy equations are ob-tained. The numerical solutions are obtained by considering an exponential dependent stretching velocity and prescribed boundary temperature on the flow directional coordinate. The effects of various physical parameters, such as Prandtl number, Grashof number, Hartmann number, porous parameter, and non-uniform heat source/sink on flow and heat transfer characteristics are presented graphically to reveal a number of interesting aspects of the physical parameter.

Chapter 9 presents an analysis of the boundary layer flow, heat and mass transfer over a stretching sheet due to nanofluids with the effects of the mag-netic field, brownian motion, thermophoresis, viscous dissipation and convec-tive boundary conditions. The transport equations used in the analysis take into account the effect of Brownian motion and thermophoresis parameters. The highly nonlinear partial differential equations governing flow, heat and mass transport are simplified using similarity transformation. The ordinary differential equations obtained are solved numerically using the Runge-Kutta-Fehlberg and Newton-Raphson schemes based on the shooting method. The solutions for velocity, temperature and nanoparticle concentration depend on parameters such as Brownian motion, thermophoresis parameter, magnetic field and viscous dissipation, which have a significant influence on controlling of the dynamics.

(18)

In Chapter 10 the linear stability of Maxwell fluid-nanofluid flow in a saturated porous layer is examined theoretically when the walls of the porous layers are subjected to time-periodic temperature modulations. A modified Darcy-Maxwell model is used to describe the fluid motion, and the nanofluid model used includes the effects of the Brownian motion. The thermal con-ductivity and viscosity are considered to be dependent on the nanoparticle volume fraction. A perturbation method that is based on a small ampli-tude of an applied temperature field is used to compute the critical value of the Rayleigh number and the wave number. The stability of the system, characterized by a critical Rayleigh number, is calculated as a function of the relaxation parameter, concentration Rayleigh number, porosity parame-ter, Lewis number, heat capacity ratio, Vada´sz number, viscosity parameparame-ter, conductivity variation parameter and frequency of modulation. Three types of temperature modulations are considered, and the effects of all three types are found to destabilize the system as compared to the unmodulated system. Chapter 11 is devoted to a study of magneto-hydrodynamic flow in a vertical double passage channel taking into account the presence of the first order chemical reaction. The governing equations are solved by using a reg-ular perturbation technique valid for small values of the Brinkman number and a differential transform method valid for all values of the Brinkman num-ber. The results are obtained for velocity, temperature and concentration. The effects of various dimensionless parameters such as the thermal Grashof number, mass Grashof number, Brinkman number, first order chemical re-action parameter, and Hartman number on the flow variables are discussed and presented graphically for open and short circuits. The validity of solu-tions obtained by the differential transform method and regular perturbation method are in good agreement for small values of the Brinkman number. Fur-ther, the effects of governing parameters on the volumetric flow rate, species concentration, total heat rate, skin friction and Nusselt number are also ob-served and tabulated.

(19)

sheet in presence of thermal radiation and magnetic field 169 6.1 Introduction . . . 169 6.2 Formulation of the Problem . . . 171 6.3 Similarity Transformations . . . 175 6.4 Numerical Solution . . . 177 6.5 Results and Disscussion . . . 178 6.6 Conclusion . . . 179 References . . . 181 7 Heat transfer in a MHD mixed convection viscoelastic fluid

flow over a stretching sheet 187 7.1 Introduction . . . 187 7.2 Mathematical formulation . . . 190 7.2.1 Solution of Momentum Equation . . . 191 7.3 Heat Transfer Analysis . . . 192 7.3.1 Prescribed Surface Temperature (PST) . . . 193 7.3.2 Prescribed Heat Flux (PHF) . . . 193 7.4 Numerical solution . . . 194 7.5 Results and Disscussions . . . 196 7.6 Conclusion . . . 201 References . . . 201

(23)

8 Heat transfer in MHD non–Darcian flow due to an exponen-tial stretching sheet embedded in a porous medium 207 8.1 Introduction . . . 207 8.2 Mathematical Formulation . . . 211 8.3 Numerical Solution . . . 214 8.4 Results and Discussion . . . 215 8.5 Conclusion . . . 221 References . . . 222 9 Heat and mass transfer in MHD boundary layer flow over

a nonlinear stretching sheet in a nanofluid with convective boundary conditions 229 9.1 Introduction . . . 229 9.2 Formulation of the Problem . . . 232 9.3 Results and Discussion . . . 234 9.4 Conclusion . . . 244 References . . . 245 10 Effect of time-periodic boundary temperature modulations

on the onset of convection in a Maxwell fluid-nanofluid sat-urated porous layer 253 10.1 Introduction . . . 253 10.2 Mathematical Formulation . . . 256 10.3 Basic State Problem . . . 258 10.4 Linear Stability Analysis . . . 259 10.5 Method of Solution . . . 261 10.6 Results and Discussion . . . 266 10.7 Conclusion . . . 276

(24)

References . . . 279 11 Effect of first order chemical reaction on magneto convection

in a vertical double passage channel 285 11.1 Introduction . . . 285 11.2 Mathematical Formulation . . . 288 11.3 Solutions . . . 290 11.3.1 Perturbation Method . . . 290 11.3.2 Basic Concept of Differential Transform Method . . . . 293 11.4 Results and Discussion . . . 294 11.5 Conclusion . . . 314 References . . . 317

(25)

List of Figures

1.1 Schematic of a polymer extrusion process . . . 36 1.2 Schematic of polymer extrusion process with an inclination . . 37 1.3 Schematic of polymer extrusion process under the influence of

gravity . . . 38 2.1 Rheogram . . . 74 3.1 Schematic representation of horizontal stretching sheet problem.114 3.2 Variation of velocity profile for Magnetic parameter with P r =

1.0, Ec = Q = 0.01. . . 121 3.3 Variation of temperature profile for Magnetic parameter with

P r = 1.0, Ec = Q = 0.01. . . 122 3.4 Variation of temperature profile for Prandtl number with M n =

1.0, Ec = Q = 0.01. . . 122 3.5 Variation of temperature profile for Eckert number with M n =

1.0, P r = 1.0, Q = 0.01. . . 123 3.6 Variation of temperature profile for uniform heat source/sink

with M n = 1.0, P r = 1.0, Ec = 0.01. . . 123 4.1 Schematic representation of a nanoliquid film on an elastic sheet.131 5.1 Variation of dimensionless film thickness β with unsteadiness

parameter S for different values of thermocapillary number M and the nanoparticle volume fraction φ (solid lines correspond to φ = 0 and dashed lines correspond to φ = 0.1) . . . 160 5.2 Effect of thermocapillary number M on the axial velocity

pro-file f0(η) . . . 160 5.3 Effect of thermocapillary number M on the temperature

(26)

6.1 Schematic representation of a liquid film on an elastic sheet . . 172 6.2 Variation of velocity profile with Magnetic parameter M n . . . 180 6.3 Variation of temperature profile with Magnetic parameter M n 180 6.4 Variation of temperature profile with Prandtl parameter P r . 180 6.5 Variation of temperature profile with Radiation parameter N r 181 7.1 Variation of temperature profile with Prandtl number P r . . . 198 7.2 Variation of temperature profile with Convection parameter Gr.198 7.3 Variation of temperature profile with Porous parameter k2 . . 198

7.4 Variation of temperature profile with Eckert number Ec . . . . 199 7.5 Variation of temperature profile with Magnetic parameter M n 199 7.6 Variation of temperature profile with viscoelastic parameter k1 199

7.7 Variation of temperature profile with space dependent heat source/sink parameter A∗ . . . 200 7.8 Variation of temperature profile with temperature dependent

heat source/sink parameter B∗. . . 200 8.1 Schematic representation of vertical stretching sheet problem . 211 8.2 Variation of velocity and temperature profile with Prandtl

number P r . . . 218 8.3 Variation of velocity and temperature profile with Grashoff

number Gr . . . 218 8.4 Variation of velocity and temperature profile with Eckert

num-ber Ec . . . 219 8.5 Variation of velocity and temperature profile with A∗ . . . 219 8.6 Variation of velocity and temperature profile with B∗ . . . 220 8.7 Variation of velocity and temperature profile profile with Porous

parameter N 1 . . . 220 8.8 Effects of magnetic field on velocity and temperature profile. . 221 9.1 Physical model of nano boundary layer flow over a nonlinear

stretching sheet . . . 232 9.2 Effect of N t and N b on temperature profiles when M n = 2,

Ec = Le = 5, P r = 5, Bi = 0.1 . . . 238 9.3 Effect of Le on temperature profiles when n = 2, M n = 2,

N t = N b = 0.1, P r = 5, Ec = 5, Bi = 0.1 . . . 238 9.4 Effect of Bi on temperature profiles when n = 1.5, M n = 2,

(27)

9.5 Effect of P r on temperature profiles when n = 1, M n = 2, N t = N b = Bi = 0.1, Le = 5, Ec = 5 . . . 239 9.6 Effect of M n on temperature profiles when n = 2, N t = N b =

Bi = 0.1, P r = Le = 5, Ec = 5 . . . 240 9.7 Effect of Eckert number on temperature profiles for different

values of n = 1.5, N t = N b = 5, P r = 1.0, Bi = 0.5, M n = 2 . 240 9.8 Effect of N t and N b on concentration profiles when n = 2,

Bi = 0.1, Le = P r = 5, M n = 1.5 . . . 241 9.9 Effect of Le on concentration profiles for different values of

n = 2, N t = N b = 0.1, P r = 5, Bi = 0.1 . . . 241 9.10 Effect of Bi on concentration profiles for different values of

n = 2, N t = N b = 0.1, P r = Le = 5 . . . 242 9.11 Effect of M n on concentration profiles for different values of

n = 2, N t = N b = Bi = 0.1, P r = Le = 5 . . . 242 9.12 Effect of nonlinear stretching parameter n on velocity profile

for various values of M n = 2, N t = N b = Bi = 0.1, P r = Le = 5 . . . 243 9.13 Effect of nonlinear stretching parameter n on temperature

pro-file for various values of M n = 1, N t = N b = Bi = 0.1, P r = Le = 5 . . . 243 10.1 Variation of R2c with ω for different values of λ1 and Rn . . . 268

10.2 Variation of R2c with ω for different values of Rn . . . 269

10.3 Variation of R2c with ω for different values of ε and Le . . . . 269

10.4 Variation of R2c with ω for different values of Rn and Le . . . 270

10.5 Variation of R2c with ω for different values of Rn and σ . . . . 270

10.6 Variation of R2c with ω for different values of Rn and Vad´asz

number V a . . . 271 10.7 Variation of R2c with ω for different values of Rn and ν . . . . 271

10.8 Variation of R2c with ω for different values of Rn and γ . . . . 272

10.9 Variation of R2c with ω for different values of Rn and λ1 . . . 272

10.10 Variation of R2c with ω for different values of Rn . . . 273

10.11 Variation of R2c with ω for different values of Rn and ε . . . 273

10.12 Variation of R2c with ω for different values of Rn and Le . . . 274

10.13 Variation of R2c with ω for different values of Rn and σ . . . 274

10.14 Variation of R2c with ω for different values of Rn and V a . . 275

10.15 Variation of R2c with ω for different values of Rn and ν . . . 275

(28)

11.1 Velocity profiles for different values of thermal Grashof number GRT at (a) y∗ = −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . 299

11.2 Temperature profiles for different values of thermal Grashof number GRT at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . . 299

11.3 Velocity profiles for different values of concentration Grashof number GRC at (a) y∗= −0.8, (b) y∗= 0, (c) y∗ = 0.8 . . . 300

11.4 Temperature profiles for different values of concentration Grashof number GRC at (a) y∗= −0.8, (b) y∗= 0, (c) y∗ = 0.8 . . . . 301

11.5 Velocity profiles for different values of Brikman number Br at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . 301 11.6 Temperature profiles for different values of Brikman number

Br at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . 302 11.7 Velocity profiles for different values of chemical reaction

pa-rameter α at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . 302 11.8 Temperature profiles for different values of chemical reaction

parameter α at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . . 303 11.9 Concentration profiles for different values of chemical reaction

parameter α at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . . 303 11.10 Velocity profiles for different values of Hartmann number M

at (a) y∗= −0.8, (b) y∗= 0, (c) y∗= 0.8 . . . 304 11.11 Temperature profiles for different values of Hartmann number

M at (a) y∗= −0.8, (b) y∗ = 0, (c) y∗= 0.8 . . . 304 11.12 Velocity profiles for different values of electric field load

pa-rameter E at (a) y∗= −0.8, (b) y∗ = 0, (c) y∗= 0.8 . . . 305 11.13 Temperature profiles for different values of electric field load

(29)

List of Tables

5.1 Rheological properties of the CMC-water solution (Lin et. al. [24]) . . . 154 5.2 Thermo-physical properties of liquid and nanoparticles (Lin

et. al. [24]) . . . 154 8.1 Nomenclature . . . 216 9.1 Nomenclature . . . 235 9.2 Comparison of results for the reduced Nusselt number −θ0(0)

and the reduced Sherwood number −φ0(0) with Khan and Pop [17] . . . 236 10.1 Nomenclature . . . 277 11.1 Comparison of velocity and temperature with Br=0 and y∗=0.0.300 11.2 Comparison of velocity and temperature with Br=0.05 and

y∗=0.0 . . . 306 11.3 Comparison of velocity and temperature with Br=0.15 and

y∗=0.0 . . . 306 11.4 Comparison of velocity and temperature with Br=0 and y∗

=-0.8... . . 307 11.5 Comparison of velocity and temperature with Br=0.05 and

y∗=-0.8 . . . 307 11.6 Comparison of velocity and temperature with Br=0.1 and

y∗=-0.8 . . . 308 11.7 Comparison of velocity and temperature with Br=0 and y∗=0.8.308 11.8 Comparison of velocity and temperature with Br=0.01 and

(30)

11.9 Comparison of velocity and temperature with Br=0.08 and y∗=0.8 . . . 309 11.10 Volumetric flow rate . . . 310 11.11 Species concentration . . . 311 11.12 Total energy flow . . . 311 11.13 Skin friction . . . 312 11.14 Skin friction . . . 313 11.15 Nomenclature . . . 315

(31)

(32)

(33)

Chapter 1 Introduction

1.1 Introduction

1.1.1 Objective and scope

The thesis addresses the problems of liquid flow due to a stretching sheet. These problems are handled either analytically or numerically depending on their complexity and feasibility of solution and interesting results are pre-sented both from the side of Mathematics and Physics. Numerical solutions are studied for coupled nonlinear differential equations arising in mixed con-vection flow through various geometries for Newtonian/ non-Newtonian flu-ids by Runge-Kutta shooting method, perturbation method and differential transform method. In the context of these problems we now present the objective and scope of the thesis.

In the era of rapidly changing technologies fluid dynamics has an impor-tant role to play. The present century has witnessed a thorough understand-ing of the principles of fluid dynamics and adopt them to many practical problems. Most of problems in fluid dynamics are inherently nonlinear. All these problems and phenomena modeled by ordinary or partial differential equations. Solutions of these differential equations are important in predict-ing the future states of the phenomena under the study.

In addition, flow and heat transfer continues to be a major field of interest to engineering and scientific researchers, as well as designers, developers and manufacturers. The applications of fluid dynamics are stretched over a broad spectrum of disciplines of science and engineering ranging from chemical en-gineering to geophysics. Chemical, aeronautical, biomedical, civil, marine

(34)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow and mechanical engineers as well as astrophysicists, space researchers, mete-orologists, physical oceanographers, physicists, applied mathematicians and geophysicists have used this knowledge to tackle a multitude of complex flow phenomena. The typical complex flows encountered by these researchers of-ten comprise of two or more phases in which the interaction between them plays a dominant role in controlling transport processes such as heat and mass exchange and reaction kinetics. A quantitative study through a proper theory is essential to understand the physics of the complex flow behavior and also to obtain invaluable scale-up information for industrial applications. The vertical channel geometry has been widely studied in heat transfer be-cause of its fundamental importance, and its many applications, including electronic cooling, and thermal environmental control of dwelling. The in-teraction between buoyancy stemming from one or more heated elements inside channel and the imposed forced flow forms the topic of the current investigation.

Nanofluids are engineered by suspending nanoparticles with average sizes below 100nm in traditional heat transfer fluids such as water, oil, and ethy-lene glycol. A very small amount of guest nanoparticles, when dispersed uniformly and suspended stably in host fluids (base fluids), can provide dra-matic improvements in the thermal properties of host fluids. Nanofluids (nanoparticle fluid suspensions) is the term coined by Choi [15] to describe this new class of nanotechnology-based heat transfer fluids that exhibit ther-mal properties superior to those of their host fluids or conventional parti-cle fluid suspensions. Nano partiparti-cles used in nano fluids have been made of various materials, such as oxide ceramics (Al2O3, CuO), nitride ceramics

(AlN, SiN ), carbide ceramics (SiC, T iC), metals (Cu, Ag, Au), semiconduc-tors (T iO2, SiC), carbon nanotubes, and composite materials such as alloyed

nanoparticles or nanoparticle corepolymer shell composites. In addition to nonmetallic, metallic, and other materials for nanoparticles, completely new materials and structures, such as materials doped with molecules in their solid-liquid interface structure, may also have desirable characteristics. The goal of nanofluids is to achieve the highest possible thermal properties at the smallest possible concentrations (preferably less than 1% by volume) by uniform dispersion and stable suspension of nanoparticles in host fluids. To achieve this goal it is vital to understand how nanoparticles enhance energy transport in liquids.

Theoretical and applied research in flow, heat, and mass transfer in porous media has received increased attention during the past four decades. This is

(35)

Introduction due to the importance of this research area in many engineering applications. Significant advances have been made in modeling fluid flow, heat, and mass transfer through a porous medium including clarification of several important physical phenomena. For example, the non-Darcy effects on momentum, energy, and mass transport in porous media have been studied in depth for various geometrical configurations and boundary conditions. Many of the research works in porous media for the past couple of decades utilize what is now commonly known as the Brinkman–Forchheimer extended Darcy model or the generalized model. Literature concerning convective flow in porous media is abundant.

Magnetohydrodynamics (MHD) is the science which deals with the mo-tion of highly conducting fluids in the presence of a magnetic field. The motion of the conducting fluid across the magnetic field generates electric currents which change the magnetic field, and the action of the magnetic field on these currents gives rise to mechanical forces which modify the flow of the fluid. The research in MHD flows was stimulated by two problems: the protection of space vehicles from aerodynamic overheating and destruc-tion during the passage through the dense layers of the atmosphere; the enhancement of the operational ability of the constructive elements of high temperature MHD generators for direct transformation of heat energy into electric current. The first problem showed that the influence of a magnetic field on ionized gases is a convenient control method for mass, heat and hydrodynamic processes. The MHD research extended gradually to new ap-plied problems. The MHD devices for liquid metals attracted the attention of metallurgist. It was shown that the effect of magnetic field could be very helpful in the modernization of technological processes. One of the ways of studying magnetohydrodynamic heat transfer field is the electro-magnetic field, which is used to control the heat transfer as in the convection flows and aerodynamic heating. Electroconducting fluid has been increasingly used in the manufacturing processes of semiconducting material such as silicon crystal or gallium arsenide.

The last two decades of the present century also witnessed a great surge in the use of liquid systems involving non-Newtonian liquid as a working medium. This encompasses in its realm complex liquids, e.g., polymeric suspensions, animal blood, liquid crystals, which have very small-sized sus-pended particles of different shapes. These particles may change shape, may shrink and expand, and moreover, they may execute rotation independent of the rotation and movement of the liquid. Due to the addition of particles the

(36)

Figure 1.1: Schematic of a polymer extrusion process

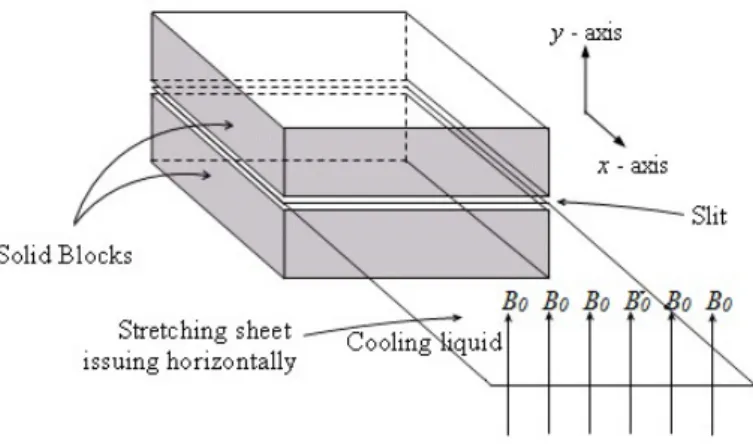
classical Navier-Stokes theory had to be re-examined. Most practical prob-lems involving these types of working liquids are non-isothermal and these thermally responding liquids have uncovered new application areas. With the above-cited view points, we now briefly discuss about the possible ap-plication situations of the problems considered in the thesis. Many chemical engineering processes like those in metallurgy and polymer extrusion Fig:1.1 (image is taken from Abel et al. [1]) involve the cooling of a molten liquid (polymer solution, molten metal, etc.) by drawing it into a cooling liquid, sometimes referred as the ambient liquid. While drawing the molten liquid into the cooling system it is sometimes stretched (as in the case of polymer-sheet-extrusion). The stretching imparts a unidirectional orientation to the extrudate, thereby improving its fluid mechanical properties (see Fisher [34]). The problem of stretching sheet is thus a fundamental one and arises in many practical situations that are similar to the polymer extrusion and metallurgical processes. Some of these are listed below:

A. Continuous stretching, rolling, manufacturing of polymer sheets. B. Drawing, annealing, tinning of copper wires.

(37)

Introduction

Figure 1.2: Schematic of polymer extrusion process with an inclination

D. Boundary Layer along a liquid film in condensation processes.

E. Manufacture of materials by extrusion process and heat-treated mate-rials traveling between a feed and wind-up rolls or conveyer belts. F. Glass blowing, paper production, crystal growing, etc.

The delicate nature of the stretching sheet problem dictates the fact that the magnitude of the stretching rate has to be small. This also ensures that the stretching material released from between the two solid blocks into the liquid continues to be a plane surface rather than a curved one. Mathematical manageability is therefore at its best in the problem.

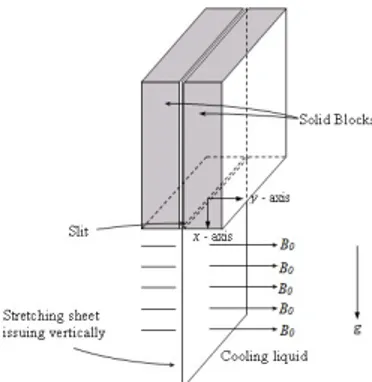
In many of the physical situations the sheet may be stretched vertically, rather than horizontally, into the cooling liquid. Under such circumstances the liquid flow and the heat transfer characteristics are determined by two mechanisms, namely the motion of stretching sheet and the buoyant force. The thermal buoyancy resulting from heating/cooling of a vertically moving stretching sheet has a large impact on the flow and heat transfer characteris-tics. This situation of flow arising due to gravity–aligned stretching is shown schematically in Fig 1.2 (image is taken from Abel et al. [1]).

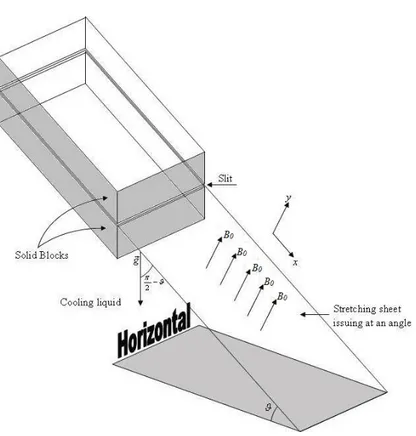
The inclined stretching is the most general way of stretching the sheet, which helps in controlling the liquid flow used for cooling purpose. This give rise to mixed convection problems (see Gebhart et al. [36]). The inclined stretching sheet problem encompasses both horizontal and vertical stretching

(38)

(39)

Introduction sheet problems as special cases. The schematic of the inclined stretching sheet problem is highlighted in Fig. 1.3 (image is taken from Abel et al. [1]).

In a polymer extrusion process, the fluid mechanical properties desired for the ultimate outcome (sheet being stretched) depend mainly on the rate of cooling. The liquid which is basically meant to cool the stretching sheet plays an important role in determining the property sought for the final product. It is imperative therefore to consider two important aspects in this physically interesting problem:

I. Proper choice of cooling liquid.

II. Regulation of the flow of the cooling liquid.

In early days water was used for the cooling purposes. But this has the drawback of rapidly quenching the heat leading to sudden solidification of the stretching sheet, i.e., water does not seem to be the ideal cooling liquid. Thus a cooling liquid which helps in quenching the heat from the sheet at a desired rate must be chosen and an optimum stretching rate has to be achieved as sudden stretching may result in spoiling the desired characteristics of the product.

A careful examination of the needs in the system suggests that it is ad-vantageous to have a controlled cooling system. An electrically-conducting Newtonian/non-Newtonian liquid seems to be a good candidate for such an application situation because its flow can be regulated by external means through a magnetic field. A weak-electrically conducting liquid can be opted as a coolant, as it induces a magnetic field of negligibly small strength (small magnetic Reynolds number limit). It is clear that the magnetohydrodynam-ics of the cooling liquid facilitates in controlling the heat transfer from the stretching sheet.

Variable properties of the cooling liquid also contribute in controlling the dynamics. The material properties such as viscosity and thermal conductivity are prone to vary with temperature gradient, especially in the boundary layer region (see Kays and Crawford [43]). Variable fluid properties have significant impact on the heat transfer characteristics of the cooling liquid.

Heat generation/absorption may become important in weak-electrically conducting cooling liquids due to the non-isothermal situation they are in and also due to the presence of cation/anion salts dissolved in them. Usually heat sinks are useful as they help in quenching the heat from the sheet.

(40)

The properties of liquid (viscosity, thermal conductivity and so on) and the external mechanisms (magnetic field, heat source/sink and so on) have significant say in the dynamics of the cooling liquid due a stretching sheet. Motivated by the practical applications of the stretching sheet problem and the above view points, the thesis presents a theoretical study of the magneto-hydrodynamic flow and heat transfer to a non-uniform property Newtonian/ non-Newtonian cooling liquid from a stretching sheet in presence of flow and temperature dependent heat source/sink. Different types of boundary con-ditions for heat transfer analysis are made use of.

The stretching sheet problem was briefly discussed thus far. The litera-ture review on the stretching sheet problem, will now be presented.

1.2 Literature survey

In 1904, when Prandtl proposed his assumptions that when viscous fluid flows past a surface, the viscous effects is dominant in a thin layer called the boundary layer, the flow may be regarded as that of an ideal fluid. The boundary layer theory had tremendous achievement to its credit and trans-formed fluid dynamics into a discipline of great engineering importance. It gives a correct predictions for resistance to motion of ships and for lift and drag on aero plane wings. The formulation of rheological equations of state was discussed by Oldroyd [70, 71]. The effect of visco-elasticity in the steady motion of some idealized visco-elastic liquids has been discussed. In 1960 Walters [96, 97] has discussed the motion of a visco-elastic liquid contained between co-axial cylinders and has given the solutions of the problem in case of materials.

Ahmed et al. [3] investigated the exact solution regarding convective heat transfer of a magnetohydrodynamic (MHD) in presence of Jeffrey fluid over a stretching surface. The effects of joule and viscous dissipation, internal heat source/sink and thermal radiation on the heat transfer characteristics are taken in account in the presence of a transverse magnetic field.

Hosain, M.L. and Bel Fdhila, R. [39] in this investigation different types of CFD methods are described briefly. Different ways to solve CFD problems are presented and their limitations are discussed and suggestions to overcome the limitations are proposed. Various methods have been identified which can significantly speed up the simulations in real time or near real time in order to use the results in the online control system for decision support during the

(41)

Literature survey ongoing process operation. Hosain, M.L., Bel Fdhila, R., Daneryd, A. [40] numerical models are developed to simulate single and multiple water jets impinging on a hot flat surface. The heat transfer from the surface to the water jets is studied. A 3D model to simulate a single jet and two jets are presented using theory and published data. A 2D axisymmetric model is developed to analyse the influence of the flow rate on the heat transfer and a correlation for the radial position of the maximum Nusselt number is formulated based on the numerical results.

Hayat et al. [41] developed a numerical model to study the three dimen-sional (3D) flow of viscous nanoliquid induced by a stretching surface. The heat and mass transfer attributes through the generalized Fourier’s and Fick’s laws, namely Cattaneo-Christov double diffusion expressions. The Buon-giorno’s model of nanofluids, Thermophoretic and Brownian motion aspects are considered. To derive convergent solutions for the velocities, temperature and concentration the optimal homotopy analysis method (OHAM) is used. Skin friction and heat and mass transfer rates at the surface are discussed in detail.

1.2.1 Stretching sheet problem involving Newtonian

liquids

Sakiadis [80, 81, 82] was the first to study a two-dimensional, axisymmetric boundary layer flow over a stretched surface moving with constant velocity. Both exact and approximate solutions were presented for a laminar flow with the latter being obtained by the integral method. Due to the entrainment of the ambient liquid, this situation represents a different class of boundary layer problems (Blasius [13]) and has a solution substantially different from that of boundary layer flow over a semi-infinite flat plate. Erickson et al. [29] extended the work of Sakiadis [80, 81, 82] to study mass transfer at the stretched sheet surface.

Crane [19] pointed out that in the polymer industry it is sometimes neces-sary to consider a stretching plastic sheet. An analytical form was presented by Crane [19] for the steady boundary layer flow of an incompressible vis-cous liquid caused solely by the linear stretching of an elastic flat sheet which moves in its own plane with a velocity varying linearly with distance from a fixed point.

(42)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow flow over a stretching surface (with suction or blowing) issuing from a thin slit. A non-isothermal moving sheet was dealt with and the temperature and concentration distribution profiles for that situation were obtained.

Banks [12] examined a class of similarity solutions of the boundary layer equations for the flow due to a stretching surface. The ordinary differen-tial equation that arises admits of a one-parameter family of solutions in much the same way the Falkner-Skan equation does. The equation is in-tegrated numerically for a number of parameter values and various results are presented. Analytical solution is also presented for a couple of values of the parameters and these, together with perturbation solutions, support the numerical results.

Grubka and Bobba [38] carried out heat transfer studies by considering the power-law variation of surface temperature. Dutta et al. [26] analyzed the temperature distribution in a flow over a stretching sheet with uniform heat flux. The governing differential equation transformed to a confluent hypergeometric differential equation and solution was obtained in terms of incomplete gamma function. It was shown that temperature at a point de-creased with the increase of Prandtl number. Dutta and Gupta [27] solved the coupled heat transfer problem involving the stretching sheet. Variation of the sheet temperature with distance from the slit was found for several values of the Prandtl number and stretching speeds. It was shown that for a fixed Prandtl number, the surface temperature decreases with an increase in the stretching speed.

Dutta [28] presented an analytical solution of the heat transfer problem for cooling of a thin stretching sheet in a viscous flow in the presence of suction or blowing. The local velocity of the sheet material was assumed to be proportional to the distance from the slit. The convergence criteria of the solution was also established. Char and Chen [17] investigated the effects of both power law surface temperature and power law heat flux variations on the heat transfer characteristics of a continuous, linearly stretching sheet subjected to suction or blowing.

Soewono et al. [86] analyzed the existence of solutions of a nonlinear boundary value problem, arising in flow and heat transfer over a stretching sheet with variable thermal conductivity and temperature-dependent heat sources or sinks. Karahalios [42] obtained an exact similarity solution of the time-dependent Navier-Stokes equation when a flat surface stretches radially. The velocity components were expressed in a power series in time up to the second-order of approximation.

(43)

Literature survey Vajravelu [93] carried out analysis of convective flow and heat transfer in a viscous heat-generating liquid near an infinite vertical stretching surface. The effects of free convection and suction or injection on the flow and heat transfer were considered. The equations of conservation of momentum, mass, and energy, which govern the flow and heat transfer, were solved numerically by using a variable order, variable step size finite-difference method. The nu-merical results obtained for the flow and heat transfer characteristics revealed an interesting behavior.

Kumaran and Ramanaiah [44] for the first time studied the viscous bound-ary layer flow over a quadratically stretching sheet. The plot of skin friction and streamline pattern as a function of the stretching parameters were dis-cussed. Magyari and Keller [55] examined both analytically and numeri-cally the heat and mass transfer in the boundary layer on an exponentially stretching continuous surface with an exponential temperature distribution. Magyari and Keller [56] studied the steady boundary layer flow induced by permeable stretching surfaces with variable temperature distribution under Reynolds analogy. Reynolds analogy makes use of the advantage of all the exact analytic solutions of the momentum and energy equations.

Magyari and Keller [57] analyzed the free laminar jets of classical hy-drodynamics that may be identified with certain boundary-layer flows in-duced by continuous surfaces immersed in quiescent incompressible liquids and stretched with well-defined velocities. Two cases were considered: (i) Schlichtings round jet of momentum flow and (ii) Schlichting-Bickley plane jet of momentum flow. By presenting an analytic solution of the flow prob-lem, it was shown that in the limiting case of a vanishing lateral mass flux, this stretching-induced flow goes over, by an adequate scaling transformation, to the well known wall jet.

Wang [94] investigated the flow due to a stretching flat boundary with partial slip and gave an exact solution of the Navier-Stokes equations. The solution belongs to a rare class of exact similarity solutions of the Navier-Stokes equation. Andersson [5] presented a slip flow past a linearly stretching sheet using the slip condition at the sheet. An exact analytical solution of the Navier-Stokes equation that is formally valid for all Reynolds numbers was found.

Magyari et al. [58, 59] examined the self-similar boundary-layer flow of a Newtonian liquid over a permeable continuous plane surface stretching with inverse linear velocity. It was shown that in order to obtain from pseudo-similarity the correct pseudo-similarity problem, in this case, the usual expression

(44)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow of the stream function a logarithmic term in the wall coordinate x must be added. The new analytical solution of a well-known boundary value problem shows that the hyperbolic-tangent solution of this problem belongs to a one-parameter family of multiple solutions, that can be expressed in terms of Airys function.

Mahapatra and Gupta [60] examined an exact similarity solution of the Navier-Stokes equation. The solution represents steady asymmetric stagnation-point flow towards a stretching surface. It is shown that the flow displays a boundary layer structure when the stretching velocity of the surface is less than the free stream velocity. On the other hand, an inverted boundary layer is formed when the surface stretching velocity exceeds the free stream veloc-ity. Temperature distribution in the flow is found when the surface is held at a constant temperature. It turns out that when the surface temperature exceeds the ambient temperature, heat flows from the surface to the liquid near the stagnation point but further away from the stagnation point heat flows from the liquid to the stretching surface.

Partha et al. [69] have examined the mixed convection flow and heat transfer from an exponentially stretching vertical surface in a quiescent liq-uid using a similarity solution. They found that the wall temperature and stretching velocity can have a specific exponential form. The influence of buoyancy along with viscous dissipation on the convective transport in the boundary layer region was analyzed in both aiding and opposing flow situa-tions.

Liao [50, 52], Liao and Pop [53] and Xu [98] have used the homotopy analysis method for nonlinear problems arising in a moving sheet. Two rules, the rule of solution expression and rule of coefficient ergodicity, were proposed which play an important role in the frame of the homotopy analysis method. An explicit analytic solution is given for the first time, with recursive formulae for coefficients.

All the above investigators, however, restricted their analysis to flow of a Newtonian liquid. In what follows we review literature on the stretching sheet problem involving a liquid with asymmetric stress.

(45)

Literature survey

1.2.2 Stretching sheet problem involving non-Newtonian

liquids

Fox et al. [29] studied the flow of a power law fluid past an inextensible flat surface moving with constant velocity in its own plane. This model, however, does not exhibit certain non-Newtonian liquid properties like normal stress difference. Rajagopal et al. [73] analyzed the flow of a second order liquid over a stretching sheet without heat transfer and presented a perturbation solution for the velocity distribution. Siddappa and Abel [78] studied the flow of a Walter’s liquid B past a stretching sheet, and obtained an analytical solution to the flow equation. Siddappa and Abel [79] also studied Walter’s liquid B flow past a stretching sheet with suction. Exact solution for the boundary-layer flow equation and energy equation were obtained. The expression for the coefficient of skin friction and boundary layer thickness was also obtained and analyzed.

Rajagopal et al. [74] studied the boundary layer flow of a second order liquid over a stretching sheet with uniform free stream and obtained some interesting results. Bujurke et al. [11] studied the heat transfer in the flow of a second order liquid, obeying Coleman and Nolls constitutive equation, over a stretching sheet.

Chen and Char [17] investigated the temperature distribution in a Wal-ter’s liquid B model over a horizontal stretching plate. The velocity of the sheet was assumed to be proportional to the distance from the slit and the sheet subjected to a variable heat flux. The solution of the heat transfer equation was expressed in terms of Kummer’s function (Abramowitz and Stegun [8]; Andrews [9]). Several closed form solutions for specific condi-tions were considered. The effect of the viscoelastic parameter and the heat flux parameter on the temperature field was also studied.

Dandapat and Gupta [24] studied flow of a second-order liquid and heat transfer effected by a stretching sheet. The influence of viscoelasticity on flow behaviour and heat transfer characteristic was examined. An analyt-ical solution was also presented for velocity and temperature distributions along with numerical results. Chang [20] obtained a closed form solution of the boundary layer equation for a particular value of the non-Newtonian parameter.

Chen et al. [21] analyzed temperature distribution in the flow of Walters liquid B over a horizontal stretching plate with constant surface tempera-ture/uniform surface heat flux. It is shown that temperature at a point

(46)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow decreases with decrease in the value of viscoelastic parameter. The dimen-sionless heat transfer coefficient and the temperature distribution in the re-gion around the stretching sheet were determined for various values of the viscoelastic parameter.

Rollins and Vajravelu [75] analyzed the heat transfer in a second order liquid over a continuous stretching surface with power law surface temper-ature/power law heat flux including the effects of internal heat generation. Two cases were studied, viz., (i) PST and (ii) PHF. The solution and heat transfer characteristics were obtained in terms of the Kummer’s function. For large values of Prandtl number a uniform approximation was given in terms of parabolic cylinder function with a boundary layer of width recip-rocal of the Prandtl number in both the PST and PHF cases. Also it was shown that no boundary layer type solution exists for small Prandtl number. Sam and Rao [76] examined the problem of heat transfer in a second order liquid over a stretching sheet. An expression was obtained for skin friction and heat transfer coefficient. Sam and Rao [77] provided two closed form solutions of the momentum equation for certain range of values of viscoelastic parameter. This brought in questions of uniqueness of the solution.

Bhatnagar [10] considered the flow of an Oldroyd-B liquid, occupying the space over an elastic sheet, due to the stretching of the sheet in the presence of a constant free-stream velocity. By introducing similarity transformation for the velocity field as well as the components of the stress tensor, the governing equations were reduced to a system of coupled non-linear ordinary differential equations. The resulting equations were solved numerically and by means of a perturbation in the Weissenberg number. A comparison of the two solutions showed good agreement.

Ariel [6] investigated the generalized Gears method for computing the flow of a second order liquid. A fourth-order predictor-corrector method was used for obtaining the numerical solution of a class of singular boundary value problems in which the coefficient of the highest derivative is a small parameter. The two-dimensional stagnation point flow of the viscoelastic liquid was computed.

Ariel [7] studied the steady laminar flow of a second grade liquid over a radially stretching sheet. The viscoelasticity of the liquid was shown to give rise to a boundary value problem in which the order of the differential equations exceeds the number of boundary conditions. It was shown that the solution exists for all values of viscoelastic parameter. A perturbation solution, valid for small viscoelastic parameter, and an asymptotic solution,

(47)

Literature survey valid for large viscoelastic parameter, were also obtained.

Regulation of the stretching sheet boundary layer flow is important from the practical point of view. Sarpakaya [83] had pointed out that some liq-uids such a nuclear fuel slurries, liquid metals, mercury amalgams, biological liquids, plastic extrusions, paper coating and lubricating oil greases have ap-plications in many areas both in the absence of as well as in the presence of a magnetic field. Since cooling liquids in most applications are known to be electrically conducting, the application of magnetic field provides a rheostatic effect on the flow. We briefly review below the literature on the magnetohydrodynamic (MHD) stretching sheet problem.

1.2.3 MHD stretching sheet problem involving

New-tonian and non-NewNew-tonian liquids

Pavlov [72] presented an exact similarity solution of the MHD boundary layer equations for the steady two-dimensional flow of an electrical conducting incompressible liquid due to the stretching of an elastic sheet in the presence of a uniform, transverse magnetic field. Chakrabarti and Gupta [23] extended the work of Pavlov [72] to study the temperature distribution in the MHD boundary layer flow, in the presence of uniform suction. A similarity solution for the velocity and heat transfer characteristics in the flow with uniform suction at the wall was considered. The equation was solved in terms of incomplete gamma function. Kumari et al. [45] studied the effects of induced magnetic field and source/sink on flow and heat transfer characteristics over a stretching surface.

Vajravelu and Nayfeh [92] studied MHD convective flow and heat transfer in a viscous heat-generating liquid near an infinite vertical stretching surface. The effect of free convection and heat generation/absorption on the flow and heat transfer characteristics were considered. The equations of conservation of momentum, mass, and energy, which govern the flow and heat transfer were solved numerically by using a variable order, variable step-size finite-difference method.

Dandapat et al. [25] investigated the stability of MHD flow of a Walters liquid B past a stretching sheet. A three-dimensional linear stability analysis was performed by means of the method of weighted residuals for disturbances of the type. It was found that the magnetic field exerts a stabilizing influence on the flow. It was observed that high wave-number disturbances were more

(48)

Mathematical Analysis of Forced Convective Flow due to Stretching Sheet and Instabilities of Natural Convective Flow effectively damped than low wavenumber modes and also that disturbances of low wave-number modes were practically uninfluenced by the viscoelasticity, whereas the influence of the magnetic field was prominent.

Andersson [4] presented an MHD flow past a stretching sheet and obtained a similarity solution for velocity and pressure of the steady two-dimensional Navier-Stokes equations. The solution for the velocity field turned out to be identical with the solution of Pavlov [72].

Chiam [22] presented a solution of the energy equation for the boundary layer flow of an electrically conducting liquid under the influence of a con-stant transverse magnetic field (suction or blowing) over a linearly stretch-ing non-isothermal flat sheet. Effects due to dissipation, stress work and heat generation were considered. Analytical solution of the resulting linear non-homogeneous boundary value problem, expressed in terms of Kummer’s functions, were presented for the case of PST as well as PHF, both of which were assumed to be quadratic functions of distance.

Kumari and Nath [47] considered the effect of the magnetic field on the stagnation point flow and heat transfer of a viscous electrically conducting liquid on a linearly stretching sheet, when the velocity of the sheet and the free stream velocity are not equal. The problem may be regarded as a combination of two problems, namely, two-dimensional stagnation-point flow and flow over a stretching sheet in an ambient liquid. Exact solution of the Navier-Stokes equation were obtained.

Takhar et al. [87] considered Newtonian flow and mass transfer on a stretching sheet with a magnetic field and chemically species. Using an im-plicit finite-difference scheme the partial differential equations governing the boundary layer flow and mass transfer were solved. The magnetic field was shown to significantly increase the surface skin friction, and to slightly reduce the surface mass transfer. The surface mass transfer was found to depend strongly on the Schmidt number and the reaction rate. The surface mass transfer for the first-order reaction was found to be more than that for sec-ond or third order reaction.

Mahapatra and Gupta [54] presented a steady two-dimensional stagnation-point flow of an incompressible viscous electrically conducting liquid over a flat deformable sheet. The velocity at a point was shown to decrease/in-crease with indecrease/in-crease in the magnetic field when the free stream velocity was less/greater than the stretching velocity. The temperature distribution in the flow was obtained for a surface held at a constant temperature. The results were obtained numerically by a finite difference method with the Thomas

Mathematical Analysis of Forced Convective Flow Due to Stretching Sheet and Instabilities of Natural Convective Flow